题目内容
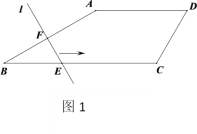
【题目】如图1，已知在平面直角坐标系
中，四边形
是矩形点
分别在
轴和
轴的正半轴上，连结
，
，
，
是
的中点.
(1)求OC的长和点的坐标；
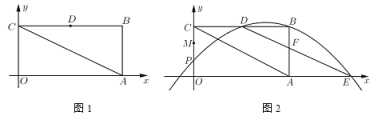
(2)如图2，
是线段
上的点，
，点
是线段
上的一个动点，经过
三点的抛物线交轴的正半轴于点
，连结
交
于点
①将
沿所在的直线翻折，若点
恰好落在上，求此时
的长和点的坐标；
②以线段
为边，在所在直线的右上方作等边
，当动点从点
运动到点时，点
也随之运动，请直接写出点运动路径的长.
【答案】(1) OC=
，点
的坐标为
；(2) ①点
的坐标为
，②
.
【解析】
（1）由OA=3，tan∠OAC=
，得OC= ，由四边形OABC是矩形，得BC=OA=3，所以CD=
BC=
，求得D（
）；
（2）①由易知得ACB=∠OAC=30°，设将△DBF沿DE所在的直线翻折后，点B恰好落在AC上的B'处，则DB'=DB=DC，∠BDF=∠B'DF，所以∠BDB'=60°，∠BDF=∠B'DF=30°，所以BF=BDtan30°=
，AF=BF=，因为∠BFD=∠AEF，所以∠B=∠FAE=90°，因此△BFD≌△AFE，AE=BD=，点E的坐标（
，0）；
②动点P在点O时，求得此时抛物线解析式为y=
，因此E（，0），直线DE： 
，F1（3，
）；当动点P从点O运动到点M时，求得此时抛物线解析式为
，所以E（6，0），直线DE：
，所以F2（3，
）；所以点F运动路径的长为
，即G运动路径的长为 ．
(1) ∵
，
∴
.
∵四边形
是矩形，
∴
.
∵是
的中点，
∴
，
∴点的坐标为.
(2) ①∵
，
∴
，
∴
.
设将
翻折后，点
落在
上的
处，
则
，
∴
，
∴
，
∴
.
∵
，
∴
.
∵
，
∴
，
∵
，
∴
.
∴
.
∴
，∴点的坐标为.
②动点P在点O时，
∵抛物线过点P（0，0）、
求得此时抛物线解析式为y=
∴E（，0），
∴直线DE： ，
∴F1（3，）；
当动点P从点O运动到点M时，
∵抛物线过点
求得此时抛物线解析式为，
∴E（6，0），
∴直线DE：y=-
∴F2（3，
）
∴点F运动路径的长为，
∵△DFG为等边三角形，
∴G运动路径的长为
