题目内容
7.阅读下面材料:小明观察一个由1×1正方形点阵组成的点阵图,图中水平与竖直方向上任意两个相邻点间的距离都是1,他发现一个有趣的问题:对于图中出现的任意两条端点在点阵上且互相不垂直的线段,都可以在点阵中找到一点构造垂直,进而求出它们相交所成锐角的正切值.
请回答:
(1)如图1,A,B,C是点阵中的三个点,请在点阵中找到点D,作出线段CD,使得CD⊥AB;
(2)如图2,线段AB与CD交于点O.为了求出∠AOD的正切值,小明在点阵中找到了点E,连接AE,恰好满足AE⊥CD于点F,再作出点阵中的其它线段,就可以构造相似三角形,经过推理和计算能够使问题得到解决.
请你帮小明计算:OC=$\frac{4\sqrt{2}}{5}$;tan∠AOD=5;
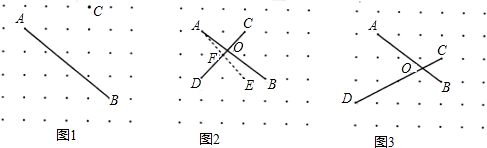
解决问题:
如图3,计算:tan∠AOD=$\frac{7}{4}$.
分析 (1)用三角板过C作AB的垂线,从而找到D的位置;
(2)连接AC、DB、AD、DE.由△ACO∽△DBO求得CO的长,由等腰直角三角形的性质可以求出AF,DF的长,从而求出OF的长,在Rt△AFO中,根据锐角三角函数的定义即可求出tan∠AOD的值;
(3)如图,连接AE、BF,则AF=$\sqrt{5}$,AB=$\sqrt{13}$,由△AOE∽△BOF,可以求出AO=$\frac{5\sqrt{13}}{7}$,在Rt△AOF中,可以求出OF=$\frac{4\sqrt{5}}{7}$,故可求得tan∠AOD.
解答 解:(1)如图所示:
线段CD即为所求.
(2)如图2所示连接AC、DB、AD.
∵AD=DE=2,
∴AE=2$\sqrt{2}$.
∵CD⊥AE,
∴DF=AF=$\sqrt{2}$.
∵AC∥BD,
∴△ACO∽△DBO.
∴CO:DO=2:3.
∴CO=$\frac{2}{5}CD=\frac{2}{5}×2\sqrt{2}=\frac{4\sqrt{2}}{5}$.
∴DO=$\frac{6\sqrt{2}}{5}$.
∴OF=$\frac{6\sqrt{2}}{5}-\sqrt{2}=\frac{\sqrt{2}}{5}$.
tan∠AOD=$\frac{AF}{AO}=\frac{\sqrt{2}}{\frac{\sqrt{2}}{5}}=5$.
(3)如图3所示:
根据图形可知:BF=2,AE=5.
由勾股定理可知:AF=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,AB=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$.
∵FB∥AE,
∴△AOE∽△BOF.
∴AO:OB=AE:FB=5:2.
∴AO=$\frac{5}{7}AB=\frac{5\sqrt{13}}{7}$.
在Rt△AOF中,OF=$\sqrt{A{O}^{2}-A{F}^{2}}=\sqrt{(\frac{5\sqrt{13}}{7})^{2}-(\sqrt{5})^{2}}$=$\frac{4\sqrt{5}}{7}$.
∴tan∠AOD=$\sqrt{5}÷\frac{4\sqrt{5}}{7}=\frac{7}{4}$.
点评 本题主要考查的是相似三角形的性质和判定、勾股定理的应用、锐角三角函数的定义,根据点阵图构造相似三角形是解题的关键.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案 如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA、CB于点E、F,点G是AD的中点,连结DE.
如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA、CB于点E、F,点G是AD的中点,连结DE.(1)求证:GE=AG=GD;
(2)试判断直线GE与⊙O的位置关系?并说明理由.
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
| 人数 | A组 | 2 | 5 | 10 | 13 | 14 | 6 |
| B组 | 4 | 4 | 16 | 2 | 12 | 12 | |
(2)根据你所学的统计知识进一步判断这两组成绩,谁优谁次,并说明理由;
(3)若要从中选出一些优秀队员参加下轮竞赛,用从哪组中选?
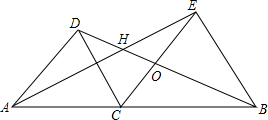 如图,在线段AB的同侧有等边△ACD和等边△CBE,AE、DB交于H.求证:DA2=DH•DB.
如图,在线段AB的同侧有等边△ACD和等边△CBE,AE、DB交于H.求证:DA2=DH•DB.
