题目内容
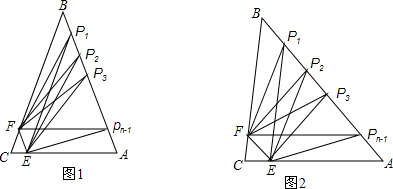
在△ABC中,E、F分别是AC、BC边上的点,P1、P2、P3、…、Pn-1是AB边的n等分点,CE=
AC,CF=
BC.如图1,若∠B=40°,AB=BC,则∠EP1F+∠EP2F+∠EP3F+…+∠EPn-1F= 度;如图2,若∠A=α,∠B=β,则∠EP1F+∠EP2F+∠EP3F+…+∠EPn-1F= (用含α,β的式子表示).
| 1 |
| n |
| 1 |
| n |

考点:相似三角形的判定与性质
专题:规律型
分析:根据已知条件得出EP1∥FB,EP2∥FP1,EP3∥FP2,…EPn-1∥FPn-2,根据两直线平行内错角相等得出∠EP1F=∠BFP1,∠EP2F=∠P1FP2,∠EP3F=∠P2FP3,…∠EPn-1F=∠Pn-2FPn-1,因为∠EP1F+∠EP2F+∠EP3F+…+∠EPn-1F=∠BFPn-1,∠BFPn-1,=∠C=70°,即可求得,同理可求得∠EP1F+∠EP2F+∠EP3F+…+∠EPn-1F=180°-α-β.
解答:解:∵P1、P2、P3、…、Pn-1是AB边的n等分点,CE=
AC,CF=
BC.
∴EP1∥FB,EP2∥FP1,EP3∥FP2,…EPn-1∥FPn-2,
∴∠EP1F=∠BFP1,∠EP2F=∠P1FP2,∠EP3F=∠P2FP3,…∠EPn-1F=∠Pn-2FPn-1,
∴∠EP1F+∠EP2F+∠EP3F+…+∠EPn-1F=∠BFPn-1,
∵∠B=40°,AB=BC,FPn-1∥AC,
∴∠BFPn-1,=∠C=70°,
同理可证:∠EP1F+∠EP2F+∠EP3F+…+∠EPn-1F=BFPn-1=∠C=180°-α-β.
| 1 |
| n |
| 1 |
| n |
∴EP1∥FB,EP2∥FP1,EP3∥FP2,…EPn-1∥FPn-2,
∴∠EP1F=∠BFP1,∠EP2F=∠P1FP2,∠EP3F=∠P2FP3,…∠EPn-1F=∠Pn-2FPn-1,
∴∠EP1F+∠EP2F+∠EP3F+…+∠EPn-1F=∠BFPn-1,
∵∠B=40°,AB=BC,FPn-1∥AC,
∴∠BFPn-1,=∠C=70°,
同理可证:∠EP1F+∠EP2F+∠EP3F+…+∠EPn-1F=BFPn-1=∠C=180°-α-β.
点评:本题考查了平行线分相等成比例定理和平行线的性质,两直线平行内错角相等是本题的关键.

练习册系列答案
相关题目
生物学家发现一种病毒的直径约为0.00000013米,0.00000013米用科学记数法表示是( )
| A、1.3×10-5 |
| B、0.13×10-6 |
| C、1.3×10-7 |
| D、1.3×10-8 |
分式
有意义时,x的取值范围是( )
| 1 |
| x(x-1) |
| A、x≠0 |
| B、x≠1 |
| C、x≠0或x≠1 |
| D、x≠0且x≠1 |
顺次连结某四边形各边中点所成的图形是菱形,则该四边形是( )
| A、矩形 | B、等腰梯形 |
| C、矩形或等腰梯形 | D、对角线相等 |
 如图,在△ABC中,AB=AC,∠A=120°,BC=12cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为
如图,在△ABC中,AB=AC,∠A=120°,BC=12cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为 如图,∠1与∠4是
如图,∠1与∠4是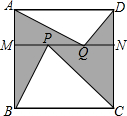 如图,正方形ABCD的边长为4,MN∥BC,分别交AB、CD于M、N,在线段MN上任取两点P、Q,那么图中阴影部分的面积是( )
如图,正方形ABCD的边长为4,MN∥BC,分别交AB、CD于M、N,在线段MN上任取两点P、Q,那么图中阴影部分的面积是( )