题目内容
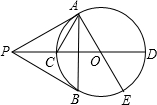 如图,PA、PB切⊙O于A、B,PO及其延长线分别交⊙O于C、D,AE为⊙O的直径,连接AB、AC,下列结论:①
如图,PA、PB切⊙O于A、B,PO及其延长线分别交⊙O于C、D,AE为⊙O的直径,连接AB、AC,下列结论:① |
| CB |
 |
| DE |
| A、①②③ | B、①②③④ |
| C、①②④ | D、②③④ |
分析:①在圆中相等圆心角所对应弧相等,
=
,连接OB,∠AOC=∠COB,所以
=
,正确.
②AO⊥AP,AB⊥PO,则∠ABP=∠PAB=∠AOP=∠DOE,正确.
③由切线性质知,∠AOC=2∠PAC=∠PAB,③正确.
④无法确定.
 |
| AC |
 |
| DE |
 |
| BC |
 |
| AC |
②AO⊥AP,AB⊥PO,则∠ABP=∠PAB=∠AOP=∠DOE,正确.
③由切线性质知,∠AOC=2∠PAC=∠PAB,③正确.
④无法确定.
解答: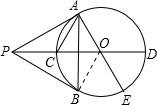 解:连接OB,如图,
解:连接OB,如图,
由切线性质知,AO⊥PA,OB⊥PB,
∴∠AOC=∠COB,
∴
=
,
∵
=
,
∴
=
,①正确;
由题知,AB⊥OP,
又∵OA⊥AP,
∴∠PAB=∠AOP=∠DOE,②正确;
由AP为切线,
∴∠AOC=∠PAB=2∠PAC,
∴AC平分∠PAB,③正确;
④条件不足.
故选A.
 解:连接OB,如图,
解:连接OB,如图,由切线性质知,AO⊥PA,OB⊥PB,
∴∠AOC=∠COB,
∴
 |
| BC |
 |
| AC |
∵
 |
| AC |
 |
| DE |
∴
 |
| CB |
 |
| DE |
由题知,AB⊥OP,
又∵OA⊥AP,
∴∠PAB=∠AOP=∠DOE,②正确;
由AP为切线,
∴∠AOC=∠PAB=2∠PAC,
∴AC平分∠PAB,③正确;
④条件不足.
故选A.
点评:本题考查了切线的性质,是基础题型.

练习册系列答案
相关题目
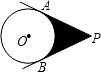 如图,PA、PB切⊙O于A、B两点,若∠APB=60°,⊙O的半径为3,则阴影部分的面积为
如图,PA、PB切⊙O于A、B两点,若∠APB=60°,⊙O的半径为3,则阴影部分的面积为 10、如图,PA、PB切⊙O于点A、B,AC是⊙O的直径,且∠BAC=35°,则∠P=
10、如图,PA、PB切⊙O于点A、B,AC是⊙O的直径,且∠BAC=35°,则∠P= 如图,PA、PB切⊙O于A、B两点,C为优
如图,PA、PB切⊙O于A、B两点,C为优 如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,分别交PA、PB于点C、D.若PA、PB的长是关于x的一元二次方程x2-mx+m-1=0的两个根,求△PCD的周长.
如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,分别交PA、PB于点C、D.若PA、PB的长是关于x的一元二次方程x2-mx+m-1=0的两个根,求△PCD的周长.