题目内容
8．
已知：四边形ABCD的面积为8068，边BA与CD的延长线交于E点，点F、G分别是四边形对角线的中点．求△EFG的面积．
分析 利用三角形的一条中线将三角形分成面积相等的两个三角形，以及面积的和与差得出S△EFG=$\frac{1}{4}$S四边形ABCD，再代入四边形ABCD的面积即可得出结果．
解答 解：连接DG，BG，如图所示：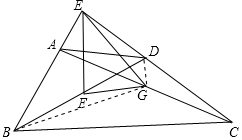
∵点G是AC中点，
∴S△AGD=S△CGD=$\frac{1}{2}$S△ACD，S△AGB=S△BGC=$\frac{1}{2}$S△ACB，
∵点F、G分别是BD、AC中点，
∴AG=GC，DF=FB，S△EGA=$\frac{1}{2}$S△EAC，S△FGB=$\frac{1}{2}$S△BDG，
S△BEF=$\frac{1}{2}$S△BED，
∴S△EFG=（S△EGA+S△AGB）-S△FGB-S△BEF，
S△EFG=（$\frac{1}{2}$S△EAC+$\frac{1}{2}$S△ACB）-$\frac{1}{2}$S△BDG-$\frac{1}{2}$S△BED，
∴2S△EFG=S△EBC-S△BDG-S△BED=S△BGC+S△CGD，
即2S△GFE=$\frac{1}{2}$S△ACD+$\frac{1}{2}$S△ACB=$\frac{1}{2}$S四边形ABCD，
∴S△GFE=$\frac{1}{4}$S四边形ABCD=$\frac{1}{4}$×8068=2017．
点评 本题主要考查了面积及等积变换、三角形的中线的性质、中点的意义、面积的和差等知识；熟练掌握三角形的一条中线分成的两个三角形的面积相等是解决问题的关键．
练习册系列答案
相关题目
已知实数a，b，c在数轴上的对应点如图所示，化简：$\root{3}{（a-b）^{3}}$-|b+c|-$\sqrt{（a-c）^{2}}$．
如图，AB是⊙O的直径，∠CAB=60°，则∠D=30度．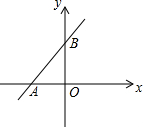
如图，直线y=5x+10与x轴、y轴交于点A，B，则△AOB的面积为10．
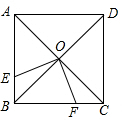如图，正方形ABCD的对角线AC、BD相交于点O，点E、F分别在边AB、BC上，且∠EOF=90°，则S四边形OEBF：S正方形ABCD=$\frac{1}{4}$．
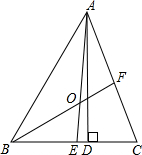如图，在△ABC中，AD是高，AE，BF是角平分线，AE和BF交于点O，∠BAC=58°，∠BOA=125°，求∠C和∠DAE的度数．
1．y=-2（x+2）2-3的顶点坐标是（ ）
| A． | （2，3） | B． | （2，-3） | C． | （-2，3） | D． | （-2，-3） |