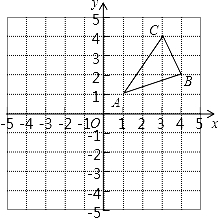
题目内容
如图,AD 是△ABC 的角平分线,DF⊥AB,垂足为 F,DE=DG,△ADG 和△AED 的面积分别 为 50 和 39,则△EDF 的面积为( )
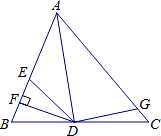
A.11 B.5.5 C.7 D.3.5
B【考点】角平分线的性质;全等三角形的判定与性质.
【专题】计算题;压轴题.
【分析】作 DM=DE 交 AC 于 M,作 DN⊥AC,利用角平分线的性质得到 DN=DF,将三角形 EDF
的面积转化为三角形 DNM 的面积来求.
【解答】解:作 DM=DE 交 AC 于 M,作 DN⊥AC 于点 N,
∵DE=DG,
∴DM=DG,
∵AD 是△ABC 的角平分线,DF⊥AB,
∴DF=DN,
在 Rt△DEF 和 Rt△DMN 中,
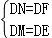 ,
,
∴Rt△DEF≌Rt△DMN(HL),
∵△ADG 和△AED 的面积分别为 50 和 39,
∴S△MDG=S△ADG﹣S△ADM=50﹣39=11,
S△DNM=S△EDF= 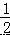 S△MDG=
S△MDG= 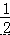 ×11=5.5.
×11=5.5.
故选 B.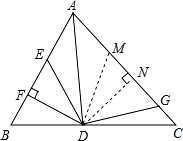
【点评】本题考查了角平分线的性质及全等三角形的判定及性质,解题的关键是正确地作出辅助线, 将所求的三角形的面积转化为另外的三角形的面积来求.

观察图形,解答问题:
(1)按下表已填写的形式填写表中的空格:
| 图① | 图② | 图③ | |
| 三个角上三个数的 积 | 1×(﹣1)×2=﹣2 | (﹣3)×(﹣4)×(﹣5)=﹣60 | (﹣2)×(﹣5)×17=170 |
| 三个角上三个数的 和 | 1+(﹣1)+2=2 | (﹣3)+(﹣4)+(﹣5)=﹣12 | (﹣2)+(﹣5)+17 |
| 积与和的商 | (﹣2)÷2=﹣1 | (﹣60)÷(﹣12)=5 | 170÷10=17 |
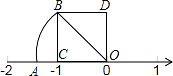
请用你发现的规律求出图④中的数 x 和图⑤中的数 y.

甲、乙两班举行电脑汉字输入速度比赛,参赛学生每分钟输入汉字的个数经统计计算后结果如下表:
| 班级 | 参加人数 | 中位数 | 方差 | 平均数 |
| 甲 | 55 | 149 | 191 | 135 |
| 乙 | 55 | 151 | 110 | 135 |
某同学根据上表分析得出如下结论:
(1)甲、乙两班学生成绩的平均水平相同;(2)乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字达150个以上为优秀);(3)甲班成绩的波动情况比乙班成绩的波动小. 上述结论中正确的是( ).
A.(1)(2)(3) B.(1)(2) C.(1)(3) D.(2)(3)
 =10
=10

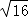
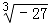 + ﹣
+ ﹣ 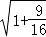 ;
;