Question

建立适当的直角坐标系，表示边长为2的正六边形的各顶点的坐标．

Answer 1

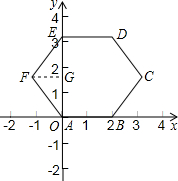解：如图所示，以A点为原点建直角坐标系，连接AE，过F作FG⊥AE，垂足是G．
∵六边形ABCDEF是正六边形，
∴∠EFA=∠FAB=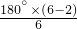=120°（多边形内角和公式=180•（n-2），正六边形各个内角相等），
在△EFA中，EF=FA
∴∠FEA=∠FAE（等边对等角），
∴∠FAE=∠FEA=（180°-120°）÷2=30°（三角形内角和是180°）．
∴∠EAB=∠FAB-∠FAE=90°即AE⊥AB．
∴y轴在经过线段AE的直线上．
在△AFE中，GE=GA（等腰三角形中，底边上的高垂直于底边，垂足是底边的中点），
在△AGF中，GF=AF•sin30°=2×=1，
EA=2AG=2AF•cos30°=2×2×=，
∴CG=2+1=3，DB=AE=2，
∵FG⊥AE，AB⊥AE，
∴FG∥AB
∴各点的坐标为：A（0，0），B（2，0），（，，．
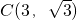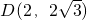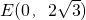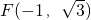分析：根据题意建立直角坐标系，再利用正六边形的内角和公式，求得内角和，利用正六边形各个角都相等的性质，求得每一个内角角度；抓住三角形的性质，求得各顶点坐标．
点评：本题是关于坐标与图形性质的题目，在解答过程中，综合运用了正六边形的性质、等腰三角形的性质、平行线的性质．所以必须牢记各种图形的性质，才会避免在做题过程中造成知识的混淆．