题目内容
7.观察下列各式:$\sqrt{1+\frac{1}{3}}$=2$\sqrt{\frac{1}{3}}$,$\sqrt{2+\frac{1}{4}}$=3$\sqrt{\frac{1}{4}}$,$\sqrt{3+\frac{1}{5}}$=4$\sqrt{\frac{1}{5}}$,…请你找出其中规律,并将第n(n≥1)个等式写出来$\sqrt{n+\frac{1}{n+2}}=(n+1)\sqrt{\frac{1}{n+2}}$.分析 根据所给例子,找到规律,即可解答.
解答 解:$\sqrt{1+\frac{1}{3}}$=(1+1)$\sqrt{\frac{1}{1+2}}$=2$\sqrt{\frac{1}{3}}$,
$\sqrt{2+\frac{1}{4}}$=(2+1)$\sqrt{\frac{1}{2+2}}$=3$\sqrt{\frac{1}{4}}$,
$\sqrt{3+\frac{1}{5}}$=(3+1)$\sqrt{\frac{1}{3+2}}$=4$\sqrt{\frac{1}{5}}$,
…
$\sqrt{n+\frac{1}{n+2}}=(n+1)\sqrt{\frac{1}{n+2}}$,
故答案为:$\sqrt{n+\frac{1}{n+2}}=(n+1)\sqrt{\frac{1}{n+2}}$.
点评 本题考查了实数平方根,解决本题的关键是找到规律.

练习册系列答案
相关题目
2.下列运算中,正确的是( )
| A. | 2$\sqrt{3}$+3$\sqrt{2}$=5$\sqrt{5}$ | B. | -a8÷a4=-a2 | C. | (3a2)3=27a6 | D. | (a2-b)2=a4-b2 |



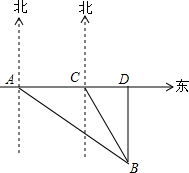 如图,新城区新建了三个商业城A,B,C,其中C在A的正东方向,在A处测得B在A的南偏东52°的方向,在C处测得B在C的南偏东26°的方向,已知A和B的距离是1000m.现有甲、乙两个工程对修建道路,甲修建一条从A到C的笔直道路AC,乙修建一条从B到直线AC最近的道路BD.求甲、乙修建的道路各是多长.(结果精确到1m)(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
如图,新城区新建了三个商业城A,B,C,其中C在A的正东方向,在A处测得B在A的南偏东52°的方向,在C处测得B在C的南偏东26°的方向,已知A和B的距离是1000m.现有甲、乙两个工程对修建道路,甲修建一条从A到C的笔直道路AC,乙修建一条从B到直线AC最近的道路BD.求甲、乙修建的道路各是多长.(结果精确到1m)(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)