题目内容
⊙O中，AB是直径，弦CD⊥AB，垂足为点E，如果CD=8，E是OB的中点，求AB的长．
解：如图，连接OC，
∵AB⊥CD，且E是OB的中点，
∴∠OCE=30°，CE=DE，
而CD=8，
∴CE=4，
∴OC=4÷
=
，
∴AB的长为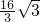
．
分析：如图，连接OC，由于AB⊥CD，且E是OB的中点，由此得到∠OCE=30°，然后接直角三角形即可求解．
点评：此题主要考查了垂径定理和勾股定理，解题首先利用垂径定理得到∠OCE=30°，然后利用勾股定理或解直角三角形即可解决问题．
∵AB⊥CD，且E是OB的中点，
∴∠OCE=30°，CE=DE，
而CD=8，
∴CE=4，
∴OC=4÷
=，∴AB的长为
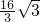．分析：如图，连接OC，由于AB⊥CD，且E是OB的中点，由此得到∠OCE=30°，然后接直角三角形即可求解．
点评：此题主要考查了垂径定理和勾股定理，解题首先利用垂径定理得到∠OCE=30°，然后利用勾股定理或解直角三角形即可解决问题．
练习册系列答案
相关题目
13、如图，在⊙O中，AB是⊙O直径，∠BAC=40°，则∠ADC的度数是
（2013•海沧区一模）已知：在⊙O中，AB是直径，AC是弦，OE⊥AC于点E，过点C作直线FC，使∠FCA=∠AOE，交AB的延长线于点D．
如图⊙O中，AB是直径，AC和AD是弦，且AD平分∠BAC，过D作AC的垂线交AC的延长线于E，
（2013•湖州一模）如图，在⊙O中，AB是直径，AD是弦，∠ADE=60°，∠C=30°．
（2012•宜宾）如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是