题目内容
 如图⊙O中,AB是直径,AC和AD是弦,且AD平分∠BAC,过D作AC的垂线交AC的延长线于E,
如图⊙O中,AB是直径,AC和AD是弦,且AD平分∠BAC,过D作AC的垂线交AC的延长线于E,(1)求证:DE是⊙O的切线.
(2)若AE=4,AB=5,求AD的长.
分析:(1)连接OD,只需证明OD⊥DE即可;
(2)利用圆周角定理:直径所对圆周角为直角和已知条件判定△AED∽△ADB,进而求出AD的长.
(2)利用圆周角定理:直径所对圆周角为直角和已知条件判定△AED∽△ADB,进而求出AD的长.
解答:(1)证明:连接OD,
∵OA=OD,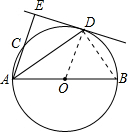
∴∠OAD=∠ODA,
又∵AD平分∠BAC,
∴∠CAD=∠DAO,
∴∠ODA=∠CAD,
∴OD∥AE,
∵AE⊥DE,
∴∠AED=90°,
∴∠AOD=90°,
∴DE是⊙O的切线;
(2)解:连接BD,
∵AB为⊙O的直径,
∴∠ADB=∠AED=90°,
∵∠CAD=∠DAO,
∴△AED∽△ADB,
∴
=
,
∴
=
∴AD=2
.
∵OA=OD,

∴∠OAD=∠ODA,
又∵AD平分∠BAC,
∴∠CAD=∠DAO,
∴∠ODA=∠CAD,
∴OD∥AE,
∵AE⊥DE,
∴∠AED=90°,
∴∠AOD=90°,
∴DE是⊙O的切线;
(2)解:连接BD,
∵AB为⊙O的直径,
∴∠ADB=∠AED=90°,
∵∠CAD=∠DAO,
∴△AED∽△ADB,
∴
| AE |
| AD |
| AD |
| AB |
∴
| 4 |
| AD |
| AD |
| 5 |
∴AD=2
| 5 |
点评:本题考查的是切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可,还考查了相似三角形的判定和性质以及圆周角定理.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目

 30、如图,在△ABC中,AB=AC,D是BC的中点,连接AD.DE⊥AB,DF⊥AC,E,F是垂足.图中共有多少对全等三角形?请直接用“≌”符号把它们分别表示出来.(不要求证明)
30、如图,在△ABC中,AB=AC,D是BC的中点,连接AD.DE⊥AB,DF⊥AC,E,F是垂足.图中共有多少对全等三角形?请直接用“≌”符号把它们分别表示出来.(不要求证明)
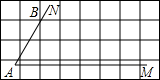 (2012•天津)“三等分任意角”是数学史上一个著名问题.已知一个角∠MAN,设∠α=
(2012•天津)“三等分任意角”是数学史上一个著名问题.已知一个角∠MAN,设∠α= 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直