题目内容
 (2013•湖州一模)如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°.
(2013•湖州一模)如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°.(1)判断直线CD是否为⊙O的切线,请说明理由;
(2)若CD=3,求BC的长.
分析:(1)根据切线的判定定理,连接OD,只需证明OD⊥CD,根据三角形的外角的性质得∠A=30°,再根据等边对等角得∠ADO=∠A,从而证明结论;
(2)在30°的直角三角形OCD中,求得OD,OC的长,则BC=OC-OB.
(2)在30°的直角三角形OCD中,求得OD,OC的长,则BC=OC-OB.
解答:解:(1)CD是⊙O的切线,理由如下:
连接OD,∵∠ADE=∠A+∠C,∠C=30°,∠ADE=60°,
∴∠A=30°,
∵OA=OD,
∴∠OAD=∠ODA=30°,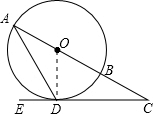
又∵∠ADE=60°,
∴∠ODE=∠ODA+∠ADE=90°,
∴DC是⊙O的切线;
(2)在Rt△ODC中,∠ODC=90°,∠C=30°,CD=3,
∵tanC=
,
∴OD=CD•tanC=3×
=
,
∴OC=2OD=2
,
∵OB=OD=3
∴BC=OC-OB=2
-3.
连接OD,∵∠ADE=∠A+∠C,∠C=30°,∠ADE=60°,
∴∠A=30°,
∵OA=OD,
∴∠OAD=∠ODA=30°,

又∵∠ADE=60°,
∴∠ODE=∠ODA+∠ADE=90°,
∴DC是⊙O的切线;
(2)在Rt△ODC中,∠ODC=90°,∠C=30°,CD=3,
∵tanC=
| OD |
| CD |
∴OD=CD•tanC=3×
| ||
| 3 |
| 3 |
∴OC=2OD=2
| 3 |
∵OB=OD=3
∴BC=OC-OB=2
| 3 |
点评:此题主要考查圆的切线的性质定理的证明、切线的判定及解直角三角形的综合运用.属于基础题.

练习册系列答案
相关题目
 (2013•湖州一模)如图,一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,它的母线长是5米,底面半径为3米,则做这把遮阳伞需用布料的面积是( )平方米(接缝不计)
(2013•湖州一模)如图,一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,它的母线长是5米,底面半径为3米,则做这把遮阳伞需用布料的面积是( )平方米(接缝不计)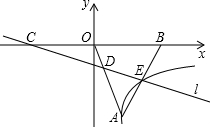 (2013•湖州一模)如图,△AOB为等边三角形,点A在第四象限,点B的坐标为(4,0),过点C(-4,0)作直线l交AO于D,交AB于E,且点E在某反比例函数x图象上,当△ADE和△DCO的面积相等时,k的值为( )
(2013•湖州一模)如图,△AOB为等边三角形,点A在第四象限,点B的坐标为(4,0),过点C(-4,0)作直线l交AO于D,交AB于E,且点E在某反比例函数x图象上,当△ADE和△DCO的面积相等时,k的值为( )