题目内容
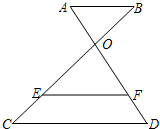
已知:线段OA⊥OB,点C为OB中点,D为线段OA上一点.连接AC,BD交于点P.
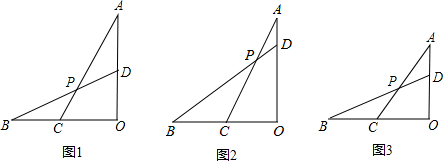
(1)如图1,当OA=OB,且
=
时,求
的值;
(2)如图2,当OA=OB,且
=
时,①
=______;②证明:∠BPC=∠A;
(3)如图3,当AD:AO:OB=1:n:2
时,直接写出tan∠BPC的值.
(1)如图1,当OA=OB,且
| AD |
| AO |
| 1 |
| 2 |
| AP |
| PC |
(2)如图2,当OA=OB,且
| AD |
| AO |
| 1 |
| 4 |
| AP |
| PC |
(3)如图3,当AD:AO:OB=1:n:2
| n |

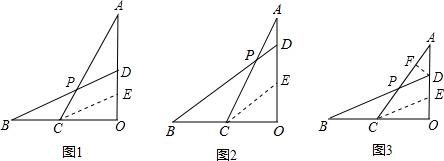
(1)过C作CE∥BD交AO于点E,如图,
∵点C为OB中点,
∴CE为△OBD的中位线,
∴DE=OE,
∵PD∥CE,
∴
=
,
又∵
=
,
∴AD=DO,
∴AD=2DE,
∴
=2;
(2)①过C作CE∥BD交AO于点E,如图,
∵点C为OB中点,
∴CE为△OBD的中位线,
∴DE=OE,
∵PD∥CE,
∴
=
,
又∵
=
,
∴DO=3AD,
∴2DE=3AD,
∴AD=
DE,
∴
=
;
②设OB=8a,
∴OA=OB=8a,OC=4a,
AD=2a,DE=OE=3a,
而OA⊥OB,
∴∠COE=90°,
在Rt△OCE中,OC=4a,OE=3a,则CE=
=5a,
∴EC=EA,
∴∠ACE=∠A,
而CE∥BD,
∴∠BPC=∠ACE,
∴∠BPC=∠A;
故答案为
;
(3)过D作DF⊥AC,垂足为F,过C作CE∥BD交AO于点E,如图,
设AD=a,则AO=na,OB=2a
,
∵点C为OB中点,
∴CO=a
,
在Rt△ACO中,AC=
=
a,
又∵Rt△ADF∽Rt△ACO,
∴AF:AO=DF:OC=AD:AC,即AF:na=DF:
a=a:
a,
∴AF=
a,DF=
,
又∵PD∥CE,
∴AP:AC=AD:AE,即AP:
a=a:
a,
∴AP=
,
∴PF=AP-AF=
a,
∴tan∠FPD=
=
=
.
∴tan∠BPC=
.
∵点C为OB中点,
∴CE为△OBD的中位线,
∴DE=OE,
∵PD∥CE,
∴
| AP |
| PC |
| AD |
| DE |
又∵
| AD |
| AO |
| 1 |
| 2 |
∴AD=DO,
∴AD=2DE,
∴
| AP |
| PC |
(2)①过C作CE∥BD交AO于点E,如图,
∵点C为OB中点,
∴CE为△OBD的中位线,
∴DE=OE,
∵PD∥CE,
∴
| AP |
| PC |
| AD |
| DE |
又∵
| AD |
| AO |
| 1 |
| 4 |
∴DO=3AD,
∴2DE=3AD,
∴AD=
| 2 |
| 3 |
∴
| AP |
| PC |
| 2 |
| 3 |
②设OB=8a,
∴OA=OB=8a,OC=4a,
AD=2a,DE=OE=3a,
而OA⊥OB,
∴∠COE=90°,
在Rt△OCE中,OC=4a,OE=3a,则CE=
| (4a)2+(3a)2 |
∴EC=EA,
∴∠ACE=∠A,
而CE∥BD,
∴∠BPC=∠ACE,
∴∠BPC=∠A;
故答案为
| 2 |
| 3 |
(3)过D作DF⊥AC,垂足为F,过C作CE∥BD交AO于点E,如图,
设AD=a,则AO=na,OB=2a
| n |
∵点C为OB中点,
∴CO=a
| n |
在Rt△ACO中,AC=
| AO2+CO2 |
| n2+n |
又∵Rt△ADF∽Rt△ACO,
∴AF:AO=DF:OC=AD:AC,即AF:na=DF:
| n |
| n2+n |
∴AF=
| ||
|
| a | ||
|
又∵PD∥CE,
∴AP:AC=AD:AE,即AP:
| n2+n |
| n+1 |
| 2 |
∴AP=
2a
| ||
|
∴PF=AP-AF=
| ||
|
∴tan∠FPD=
| FD |
| PF |
| 1 | ||
|
| ||
| n |
∴tan∠BPC=
| ||
| n |


练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目