题目内容
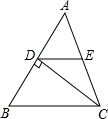
如图,已知△ABC中,AB=AC,AB边上的垂直平分线DE交AC于点E,D为垂足,若∠ABE:∠EBC=2:1,则∠A=__________.

45°.
【考点】线段垂直平分线的性质;等腰三角形的性质.
【分析】利用线段垂直平分线的性质可求得∠A=∠ABE,结合等腰三角形可求得∠C=∠ABC,结合条件可得到∠A和∠C的关系,在△ABC中利用三角形内角和可求得∠A.
【解答】解:∵AB=AC,
∴∠ABC=∠C,
∵E在线段AB的垂直平分线上,
∴EA=EB,
∴∠ABE=∠A=2∠EBC,
∴∠ABC=∠ABE+∠EBC=∠A+ ∠A,
∠A,
∵∠A+∠ABC+∠C=180°,
∴∠A+2(∠A+ ∠A)=180°,
∠A)=180°,
∴∠A=45°,
故答案为:45°.
【点评】本题主要考查线段垂直平分线的性质及等腰三角形的性质,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.注意三角形内角和定理的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 EF,AC=DF
EF,AC=DF
 B.
B. C.
C. D.
D.
 的自变量x的取值范围是__________.
的自变量x的取值范围是__________.