题目内容
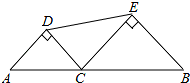 如图,线段AB的长为2,C为线段AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE.
如图,线段AB的长为2,C为线段AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE.(1)设DE的长为y,AC的长为x,求出y与x的函数关系式;
(2)求出DE的最小值.
考点:二次函数的应用
专题:
分析:(1)设AC=x,则BC=2-x,然后分别表示出DC、EC,继而在RT△DCE中,利用勾股定理求出DE长度的表达式;
(2)利用函数的性质进行解答即可.
(2)利用函数的性质进行解答即可.
解答:解:如图,
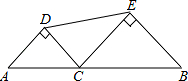
设AC=x,则BC=2-x,
∵△ACD和△BCE分别是等腰直角三角形,
∴∠DCA=45°,∠ECB=45°,DC=
x,CE=
(2-x),
∴∠DCE=90°,
故DE2=DC2+CE2=
x2+
(2-x)2=x2-2x+2=(x-1)2+1,
∴y=
.
(2)y=
当x=1时,DE取得最小值,DE也取得最小值,最小值为1.

设AC=x,则BC=2-x,
∵△ACD和△BCE分别是等腰直角三角形,
∴∠DCA=45°,∠ECB=45°,DC=
| ||
| 2 |
| ||
| 2 |
∴∠DCE=90°,
故DE2=DC2+CE2=
| 1 |
| 2 |
| 1 |
| 2 |
∴y=
| (x-1)2+1 |
(2)y=
| (x-1)2+1 |
当x=1时,DE取得最小值,DE也取得最小值,最小值为1.
点评:此题考查了二次函数最值及等腰直角三角形,难度不大,关键是表示出DC、CE,得出DE的表达式,还要求我们掌握配方法求二次函数最值.

练习册系列答案
相关题目
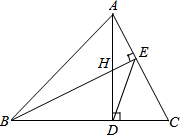 如图所示,△ABC的高AD、BE相交于点H,若BH=AC,则下列结论:
如图所示,△ABC的高AD、BE相交于点H,若BH=AC,则下列结论:①AE=CE;②∠ABC=45°;③DH=DC;④∠CED=45°
成立的有( )
| A、①② | B、①②③ |
| C、②③④ | D、①②③④ |
