题目内容
8.填空:(1)$\frac{m+n}{{m}^{2}{-n}^{2}}$=$\frac{1}{()}$;
(2)$\frac{{a}^{2}-2ab{+b}^{2}}{{a}^{2}{-b}^{2}}$=$\frac{()}{a+b}$;
(3)$\frac{x+y}{3y}$=$\frac{{x}^{2}{-y}^{2}}{()}$.
分析 (1)对分母:利用平方差公式进行因式分解;
(2)分子:完全平方公式进行因式分解;分子:利用平方差公式进行因式分解;
(3)分子、分母同时乘以(x-y).
解答 解:(1)原式=$\frac{m+n}{(m+n)(m-n)}$=$\frac{1}{m-n}$;
(2)原式=$\frac{(a-b)^{2}}{(a+b)(a-b)}$=$\frac{a-b}{a+b}$;
(3)分子分母同时乘以(x-y),得
$\frac{(x+y)(x-y)}{3y(x-y)}$=$\frac{{x}^{2}-{y}^{2}}{3y(x-y)}$.
点评 本题考查了约分.约分时,分子与分母都必须是乘积式,如果是多项式的,必须先分解因式.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
16.某市举行中学生“奋发有为建小康”演讲比赛,某同学将选手的得分情况进行统计,绘成如图所示的得分成绩统计图,下列四个论断:①众数为6分;②有8名选手的成绩高于8分;③中位数是8分;④得6分和9分的人数一样多,其中正确的是( )
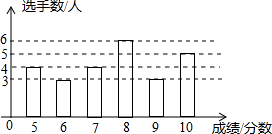

| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①②③④ |
18.下列各式中,互为相反数的两个数是( )
| A. | -5与$\frac{1}{5}$ | B. | |-$\frac{1}{2}$|与$\frac{1}{2}$ | C. | -2$\frac{1}{2}$与-0.4 | D. | -(-5)与-5 |
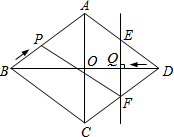 已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题: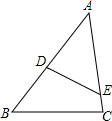 如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,如果AE=4cm,△ADE的面积是4cm2,四边形BCED的面积是5cm2,那么AB的长是6cm.
如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,如果AE=4cm,△ADE的面积是4cm2,四边形BCED的面积是5cm2,那么AB的长是6cm.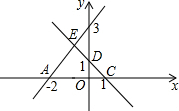 如图,直线AB分别与x轴、y轴交于点A(-2,0),B(0,3).直线CD分别与x轴、y轴交于点C(1,0),D(0,1),与直线AB交于点E.求点E的坐标.
如图,直线AB分别与x轴、y轴交于点A(-2,0),B(0,3).直线CD分别与x轴、y轴交于点C(1,0),D(0,1),与直线AB交于点E.求点E的坐标.