题目内容
18.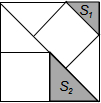 有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2=4:9.
有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2=4:9.
分析 设大正方形的边长为x,再根据相似的性质求出S1、S2与正方形面积的关系,然后进行计算即可得出答案.
解答 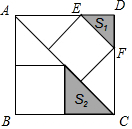 解:设大正方形的边长为x,根据图形可得:
解:设大正方形的边长为x,根据图形可得:
∵$\frac{EF}{AC}$=$\frac{1}{3}$,
∴$\frac{{S}_{1}}{{S}_{△DAC}}$=$\frac{1}{9}$,
∴$\frac{{S}_{1}}{{S}_{正方形ABCD}}$=$\frac{1}{18}$,
∴S1=$\frac{1}{18}$S正方形ABCD,
∴S1=$\frac{1}{18}$x2,
∵$\frac{{S}_{2}}{{S}_{△ABC}}$=$\frac{1}{4}$,
∴$\frac{{S}_{2}}{{S}_{正方形ABCD}}$=$\frac{1}{8}$,
∴S2=$\frac{1}{8}$S正方形ABCD,
∴S2=$\frac{1}{8}$x2,
∴S1:S2=$\frac{1}{18}$x2:$\frac{1}{8}$x2=4:9.
故答案是:4:9.
点评 此题考查了正方形的性质,用到的知识点是正方形的性质、相似三角形的性质、正方形的面积公式,关键是根据题意求出S1、S2与正方形面积的关系.

练习册系列答案
相关题目
8.若w=9-($\frac{n}{m}$+1)2,当W有最大值为P时,则3P+2m+2n的值为( )
| A. | 25 | B. | 27 | C. | 9 | D. | 不能确定 |
6.把(+12)-(-18)+(-7)+(-15)写成省略加号的和的形式是( )
| A. | 12-8-7+15 | B. | -12+18+7-15 | C. | 12+18+7-15 | D. | 12+18-7-15 |
3. 如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=8,则图中阴影部分的面积是( )
如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=8,则图中阴影部分的面积是( )
 如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=8,则图中阴影部分的面积是( )
如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=8,则图中阴影部分的面积是( )| A. | 8π | B. | 4π | C. | 64π | D. | 16π |
10.若一个正数的两个平方根为a+1和2a-7,则这个正数是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
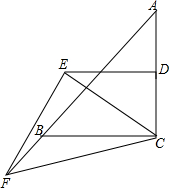 如图,△ABC为等腰Rt△,∠ACB=90°,D为AC中点,F为AB延长线上一点,作DE∥BC,且∠ECF=45°,说明CE、EF的关系.
如图,△ABC为等腰Rt△,∠ACB=90°,D为AC中点,F为AB延长线上一点,作DE∥BC,且∠ECF=45°,说明CE、EF的关系. 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连接CD,给出五个结论:①∠CAD=∠CBD;②S△DBC=S△AEC;③∠ADC=45°;④AC+CE=AB;⑤CE=2MC,其中正确的结论有( )
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连接CD,给出五个结论:①∠CAD=∠CBD;②S△DBC=S△AEC;③∠ADC=45°;④AC+CE=AB;⑤CE=2MC,其中正确的结论有( )