题目内容
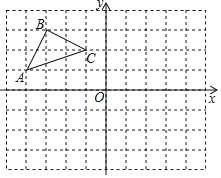
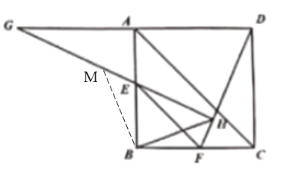
【题目】如图,已知正方形![]() (四边相等,四个角都是直角),点
(四边相等,四个角都是直角),点![]() 为边
为边![]() 上异于点
上异于点![]() 的一动点,
的一动点,![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 延长线上一定点,满足
延长线上一定点,满足![]() ,
,![]() 的延长线与
的延长线与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
(1)判断![]() 是 三角形.
是 三角形.
(2)求证: ![]() ≌
≌![]() .
.
(3)探究![]() 是否为定值?如果是定值,请说明理由,并求出该定值;如果不是定值,请说明理由.
是否为定值?如果是定值,请说明理由,并求出该定值;如果不是定值,请说明理由.

【答案】(1)等腰直角;(2)证明见解析;(3)![]() ,为定值.
,为定值.
【解析】
(1)根据正方形性质证得∠BAC=∠BCA,然后再根据![]() 得出∠BEF=∠BAC,∠BFE=∠BCA,即可证得
得出∠BEF=∠BAC,∠BFE=∠BCA,即可证得![]() 是等腰直角三角形;
是等腰直角三角形;
(2)根据等腰直角三角形得出![]() ,然后求出四边形
,然后求出四边形![]() 为正方形,即可得出答案;
为正方形,即可得出答案;
(3)在![]() 上截取
上截取![]() ,根据(2)中的结论可求出
,根据(2)中的结论可求出![]() ,又因为
,又因为![]() ≌
≌![]() ≌
≌![]() ,
,![]() ,
,![]() ,所以证得
,所以证得![]() 为等腰直角三角形,得出
为等腰直角三角形,得出![]() .
.
解:(1) ∵四边形![]() 是正方形,AC为对角线,
是正方形,AC为对角线,
∴∠BAC=∠BCA,
又∵![]() ,
,
∴∠BEF=∠BAC,∠BFE=∠BCA,
则∠BEF=∠BFE,
∵正方形![]() 四个角为直角,
四个角为直角,
∴![]() 是等腰直角三角形;
是等腰直角三角形;
(2)∵![]() 和
和![]() 为等腰直角三角形
为等腰直角三角形
∴![]() ,
,
∴![]() ,即是
,即是![]() ,
,
∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,![]() ,
,
∴![]() ≌
≌![]() (
(![]() );
);
(3)在![]() 上截取
上截取![]()
∵![]() ≌
≌![]()
∴![]()
∴![]()
即是![]()
∵![]() 为等腰直角三角形
为等腰直角三角形
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]() ≌
≌![]()
∴![]() ,
,![]()
∵![]()
∴![]() 即是
即是![]()
∴![]() 为等腰直角三角形,
为等腰直角三角形,![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目