题目内容
 如图,已知抛物线
如图,已知抛物线 的内部有正方形ABCD正方形EFGH正方形MNPQ,其中每个正方形均有两个顶点在抛物线上,已知正方形ABCD的边长为3,则正方形MNPQ的边长为________.
的内部有正方形ABCD正方形EFGH正方形MNPQ,其中每个正方形均有两个顶点在抛物线上,已知正方形ABCD的边长为3,则正方形MNPQ的边长为________.
 -4
-4分析:根据题意求出C、D的坐标,代入抛物线求出c,设正方形EFGH的边长是2a,正方形MNPQ的边长是2b,得出H、Q的坐标,代入抛物线,能求出b的值,即可求出答案.
解答:根据题意得:C的坐标是(-
 ,3),D的坐标是(
,3),D的坐标是( ,3),
,3),代入y=-
 x2+c得:3=-
x2+c得:3=- ×
×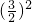 +c,
+c,解得:c=
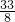 ,
,∴抛物线的解析式是y=-
 x2+
x2+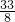 ,
,设正方形EFGH的边长是2a,正方形MNPQ的边长是2b,
则H(a,3+2a),Q(b,3+2a+2b),
代入抛物线得:
3+2a=-
 a2+
a2+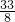 ,
,a=
 ,
,3+2a+2b=-
 b2+
b2+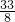 ,
,b=
 ,
,∴正方形MNPQ的边长是2b=-4+
 =
= -4,
-4,故答案为:
 -4.
-4.点评:本题考查了二次函数图象上点的坐标特征和正方形的性质的应用,通过做此题能培养学生分析问题的能力,同时培养了学生观察能力和计算能力,是一道比较好的计算题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
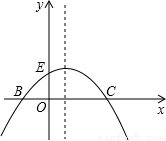
 (2012•黄冈)如图,已知抛物线的方程C1:y=-
(2012•黄冈)如图,已知抛物线的方程C1:y=- (x+2)(x﹣m)(m>0)与x轴相交于点B、C,与y轴相交于点E,且点B在点C的左侧.
(x+2)(x﹣m)(m>0)与x轴相交于点B、C,与y轴相交于点E,且点B在点C的左侧.
 (x+2)(x-m)(m>0)与x轴相交于点B、C,与y轴相交于点E,且点B在点C的左侧.
(x+2)(x-m)(m>0)与x轴相交于点B、C,与y轴相交于点E,且点B在点C的左侧.
 (x+2)(x-m)(m>0)与x轴相交于点B、C,与y轴相交于点E,且点B在点C的左侧.
(x+2)(x-m)(m>0)与x轴相交于点B、C,与y轴相交于点E,且点B在点C的左侧.
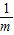 (x+2)(x-m)(m>0)与x轴相交于点B、C,与y轴相交于点E,且点B在点C的左侧.
(x+2)(x-m)(m>0)与x轴相交于点B、C,与y轴相交于点E,且点B在点C的左侧.