题目内容
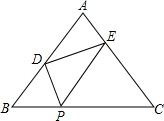如图，在△ABC中，AB=AC=5，BC=6，P是BC上一点，且BP=2，将一个大小与∠B相等的角的顶点放在P 点，然后将这个角绕P点转动，使角的两边始终分别与AB、AC相交，交点为D、E．（1）求证△BPD∽△CEP．
（2）是否存在这样的位置，使PD⊥DE？若存在，求出BD的长；若不存在，说明理由．
考点：相似三角形的判定与性质
专题：
分析：（1）先由AB=AC，得出∠B=∠C，再根据角的和差及三角形外角的性质得出∠DPC=∠DPE+∠EPC=∠B+∠BDP，又∠DPE=∠B，那么∠EPC=∠BDP，根据两角对应相等的两三角形相似即可证明△BPD∽△CEP；
（2）作AH⊥BC于H．根据等腰三角形三线合一的性质得出BH=HC=
BC=3．在Rt△ABH和Rt△PDE中，由∠B=∠DPE，根据余弦函数的定义得到
=
=
，
由（1）△BPD∽△CEP，得出
=
=
，又PC=BC-BP=6-2=4，那么BD=
．
（2）作AH⊥BC于H．根据等腰三角形三线合一的性质得出BH=HC=
| 1 |
| 2 |
| BH |
| AB |
| PD |
| PE |
| 3 |
| 5 |
由（1）△BPD∽△CEP，得出
| BD |
| CP |
| PD |
| PE |
| 3 |
| 5 |
| 12 |
| 5 |
解答：解：（1）∵AB=AC，
∴∠B=∠C．
∵∠DPC=∠DPE+∠EPC=∠B+∠BDP，∠DPE=∠B，
∴∠EPC=∠BDP．
在△BPD与△CEP中，
，
∴△BPD∽△CEP；
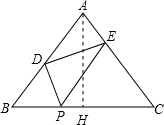（2）作AH⊥BC于H．
∵AB=AC，AH⊥BC于H，
∴BH=HC=
BC=3．
∵在Rt△ABH和Rt△PDE中，∠B=∠DPE，
∴cos∠B=cos∠DPE，
∴
=
=
，
∵△BPD∽△CEP，
∴
=
=
，
又∵PC=BC-BP=6-2=4，
∴BD=
．
∴∠B=∠C．
∵∠DPC=∠DPE+∠EPC=∠B+∠BDP，∠DPE=∠B，
∴∠EPC=∠BDP．
在△BPD与△CEP中，
|
∴△BPD∽△CEP；
（2）作AH⊥BC于H．∵AB=AC，AH⊥BC于H，
∴BH=HC=
| 1 |
| 2 |
∵在Rt△ABH和Rt△PDE中，∠B=∠DPE，
∴cos∠B=cos∠DPE，
∴
| BH |
| AB |
| PD |
| PE |
| 3 |
| 5 |
∵△BPD∽△CEP，
∴
| BD |
| CP |
| PD |
| PE |
| 3 |
| 5 |
又∵PC=BC-BP=6-2=4，
∴BD=
| 12 |
| 5 |
点评：本题考查了相似三角形的判定与性质，等腰三角形的性质，三角形外角的性质，锐角三角函数的定义，难度适中．准确作出辅助线是解题的关键．
练习册系列答案
相关题目
已知，如图，在△ABC中，∠ABC=68°，∠ACB=50°，BE、CF是两边AC、AB