题目内容
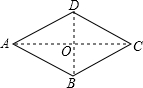 如图,菱形ABCD中,∠ADC=120°,AB=10,则BD=________AC=________,菱形ABCD的面积=________.
如图,菱形ABCD中,∠ADC=120°,AB=10,则BD=________AC=________,菱形ABCD的面积=________.
10 10 50
50
分析:根据∠ADC=120°,可判断出△ABD是等边三角形,从而得出BD,在Rt△AOB中,可求出AO,继而得出AC,再由菱形的面积=对角线乘积的一半即可得出面积.
解答:∵四边形ABCD是菱形,∠ADC=120°,
∴∠DAB=60°,
∴△ABD是等边三角形,
∴BD=AB=10,
在Rt△AOB中,AO= =5
=5 ,
,
∴AC=2AO=10 ,
,
∴S菱形ABCD= AC×BD=50
AC×BD=50 .
.
故答案为:10、10 、50
、50 .
.
点评:本题考查了菱形的性质,注意掌握菱形的四边相等,菱形的面积=对角线乘积的一半.
 50
50
分析:根据∠ADC=120°,可判断出△ABD是等边三角形,从而得出BD,在Rt△AOB中,可求出AO,继而得出AC,再由菱形的面积=对角线乘积的一半即可得出面积.
解答:∵四边形ABCD是菱形,∠ADC=120°,
∴∠DAB=60°,
∴△ABD是等边三角形,
∴BD=AB=10,
在Rt△AOB中,AO=
 =5
=5 ,
,∴AC=2AO=10
 ,
,∴S菱形ABCD=
 AC×BD=50
AC×BD=50 .
.故答案为:10、10
 、50
、50 .
.点评:本题考查了菱形的性质,注意掌握菱形的四边相等,菱形的面积=对角线乘积的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
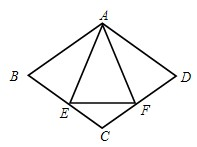 26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
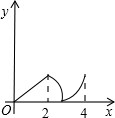
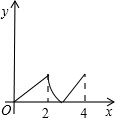
26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF. 如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )
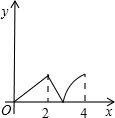
如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )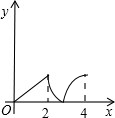
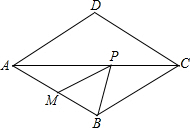 如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2
如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2 如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm.
如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm. 如图,菱形ABCD中,∠ADC=120°,AB=10,
如图,菱形ABCD中,∠ADC=120°,AB=10,