题目内容
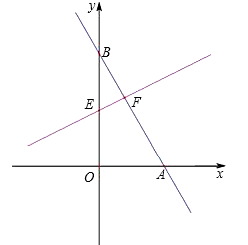
如图,直线AB分别x,y轴正半轴相交于A(a,0)和B(0,b),直 线
线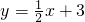 交于y轴与点E,交AB于点F
交于y轴与点E,交AB于点F
(1)当a=6,b=6时,求四边形EOAF的面积
(2)若F为线段AB的中点,且AB= 时,求证:∠BEF=∠BAO.
时,求证:∠BEF=∠BAO.
(1)解: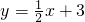 ,
,
当x=0时,y=3,
∴E(0,3),
设直线AB的解析式是y=kx+b,
把A(6,0),B(0,6)代入y=kx+b得: ,
,
解得: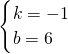
∴直线AB的函数关系式是y=-x+6
直线EF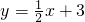 和直线AB交于点F,方程组
和直线AB交于点F,方程组 的解是
的解是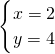 ,
,
∴F(2,4),
S四边形EOAF=S△OAB-S△EFB,
= ×6×6-
×6×6- ×(6-3)×2,
×(6-3)×2,
=15.
所以四边形EOAF的面积是15.
(2)解:∵F为线段AB的中点,由三角形中位线定理得F( a,
a, b),
b),
又∵F在直线EF: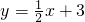 上,
上,
∴ ×
× a+3=
a+3= b,
b,
a=2b-12 ①
又∵AB=
∴a2+b2= ,
,
∴(2b-12)2+b2=80,
整理得:5b2-48b+64=0,
解得b1= ,b2=8,
,b2=8,
当b= 时,a<0,不合题意,∴b=
时,a<0,不合题意,∴b= (舍去),
(舍去),
当b=8时,a=4
∴A(4,0)B(0,8),
∴OE=3,BE=5
连接EA,在RT△OAE中,OE=3,OA=4,
∴EA=5
∴EA=BE=5
∴△BEA是等腰三角形,
又∵F为线段AB的中点
∴EF⊥AB,
∴∠BEF=90°-∠EBF,
∠BAO=90°-∠OBA,
∵∠EBF=∠OBA
∴∠BEF=∠BAO.
分析:(1)小题先求出直线AB的解析式,再求出与直线EF的交点F的坐标(2,4),利用面积公式计算即可.(2)小题利用三角形的中位线性质和勾股定理求出a b的值,连接AE,证出AE=BE,进而得到EF⊥AB,利用角之间的关系即可出答案.
点评:解本题的关键是能灵活运用一次函数的性质,能根据点的坐标求解析式,或利用解析式求特殊点的坐标,进一步求出线段长,再根据求出条件证明几何问题,
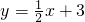 ,
,当x=0时,y=3,
∴E(0,3),
设直线AB的解析式是y=kx+b,
把A(6,0),B(0,6)代入y=kx+b得:
 ,
,解得:
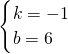
∴直线AB的函数关系式是y=-x+6
直线EF
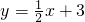 和直线AB交于点F,方程组
和直线AB交于点F,方程组 的解是
的解是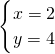 ,
,∴F(2,4),
S四边形EOAF=S△OAB-S△EFB,
=
 ×6×6-
×6×6- ×(6-3)×2,
×(6-3)×2,=15.
所以四边形EOAF的面积是15.
(2)解:∵F为线段AB的中点,由三角形中位线定理得F(
 a,
a, b),
b),又∵F在直线EF:
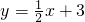 上,
上,∴
 ×
× a+3=
a+3= b,
b,a=2b-12 ①
又∵AB=

∴a2+b2=
 ,
,∴(2b-12)2+b2=80,
整理得:5b2-48b+64=0,
解得b1=
 ,b2=8,
,b2=8,当b=
 时,a<0,不合题意,∴b=
时,a<0,不合题意,∴b= (舍去),
(舍去),当b=8时,a=4
∴A(4,0)B(0,8),
∴OE=3,BE=5
连接EA,在RT△OAE中,OE=3,OA=4,
∴EA=5
∴EA=BE=5
∴△BEA是等腰三角形,
又∵F为线段AB的中点
∴EF⊥AB,
∴∠BEF=90°-∠EBF,
∠BAO=90°-∠OBA,
∵∠EBF=∠OBA
∴∠BEF=∠BAO.
分析:(1)小题先求出直线AB的解析式,再求出与直线EF的交点F的坐标(2,4),利用面积公式计算即可.(2)小题利用三角形的中位线性质和勾股定理求出a b的值,连接AE,证出AE=BE,进而得到EF⊥AB,利用角之间的关系即可出答案.
点评:解本题的关键是能灵活运用一次函数的性质,能根据点的坐标求解析式,或利用解析式求特殊点的坐标,进一步求出线段长,再根据求出条件证明几何问题,

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 线
线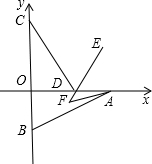 轴正半轴).
轴正半轴). 如图,直线AB分别与x轴、y轴交于点A(0,3)和点B(-1,0),求直线AB的解析式:
如图,直线AB分别与x轴、y轴交于点A(0,3)和点B(-1,0),求直线AB的解析式: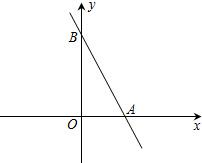 如图,直线AB分别与x轴、y轴相交于点A和点B,如果A(2,0),B(0,4)线段CD两端点在坐标轴上滑动(C点在y轴上,D点在x轴上),且CD=AB.
如图,直线AB分别与x轴、y轴相交于点A和点B,如果A(2,0),B(0,4)线段CD两端点在坐标轴上滑动(C点在y轴上,D点在x轴上),且CD=AB. 如图.直线AB分别交y轴,x轴于A,B两点,已知A(0,2
如图.直线AB分别交y轴,x轴于A,B两点,已知A(0,2