题目内容
18.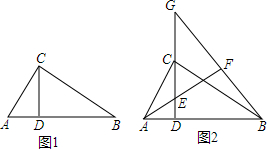 如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D;
如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D;(1)求证:△ACD∽△CBD;
(2)如图2,延长DC至点G,联结BG,过点A作AF⊥BG,垂足为F,AF交CD于点E,求证:CD2=DE•DG.
分析 (1)根据垂直的定义得到∠ADC=∠CDB=90°,根据余角的性质得到∠ACD=∠B,由于∠ADC=∠CDB,即可得到结论;
(2)根据∠ACB=90°,CD⊥AB,得到∠CAD=∠BCD,推出Rt△ACD∽Rt△CBD,于是得到CD2=AD•BD,根据AF⊥BG,GD⊥AB,证得∠EDA=∠EFG=∠GDP=90°,推出△BGD∽△ADE,于是得到AD•BD=DG•DE即可得到结论.
解答 证明:(1)∵CD⊥AB,
∴∠ADC=∠CDB=90°,
∴∠BCD+∠B=90°,
∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∴∠ACD=∠B,
又∵∠ADC=∠CDB,
∴△ACD∽△CBD;
(2)∵AF⊥BG,
∴∠AFB=90°,
∴∠FAB+∠GBA=90°,
∵∠GDB=90°,
∴∠G+∠GBA=90°,
∴∠G=∠FAB,
又∵∠ADE=∠GDB=90°,
∴△ADE∽△GDB,
∴$\frac{AD}{GD}=\frac{DE}{BD}$,
∴AD•BD=DE•DG,
∵△ACD∽△CBD,
∴$\frac{AD}{CD}=\frac{CD}{BD}$,
∴CD2=AD•BD,
∴CD2=DE•DG.
点评 此题主要考查的是相似三角形的判定和性质,垂直的定义,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
6.已知$\frac{a}{b}$=$\frac{2}{3}$,那么$\frac{a}{a+b}$的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
3.P是△ABC一边上的一点(P不与A、B、C重合),过点P的一条直线截△ABC,如果截得的三角形与△ABC相似,我们称这条直线为过点P的△ABC的“相似线”.Rt△ABC中,∠C=90°,∠A=30°,当点P为AC的中点时,过点P的△ABC的“相似线”最多有几条?( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
7.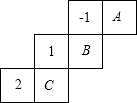 如图是一个正方体的包装盒的展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( )
如图是一个正方体的包装盒的展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( )
 如图是一个正方体的包装盒的展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( )
如图是一个正方体的包装盒的展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( )| A. | -1,-2,1 | B. | -1,1,-2 | C. | -2,-1,1 | D. | 1,-1,-2 |
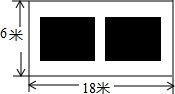 某小区在绿化工程中有一块长为18m、宽为6m的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为60m2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度.
某小区在绿化工程中有一块长为18m、宽为6m的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为60m2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度.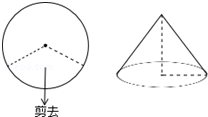 如图,圣诞节快到了,小雪准备在一块半径为9cm的 红布上剪掉三分之一圆周,然后用剩下的部分做成一个圣诞帽,则这个圣诞帽的高为3$\sqrt{5}$cm.
如图,圣诞节快到了,小雪准备在一块半径为9cm的 红布上剪掉三分之一圆周,然后用剩下的部分做成一个圣诞帽,则这个圣诞帽的高为3$\sqrt{5}$cm.