题目内容
抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3).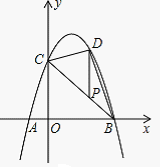
(1)求抛物线的解析式;
(2)求点B的坐标及直线BC的解析式;
(3)如图,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,求△BDC的面积的最大值。
(1)抛物线解析式为y=-x2+2x+3。(2)直线BC的解析式为y=-x+3
(3)当 时,△BDC的面积最大值是
时,△BDC的面积最大值是
解析试题分析:解:(1)∵A(-1,0),C(0,3)在抛物线y=-x2+bx+c上,
∴
∴解得 
∴抛物线解析式为y=-x2+2x+3。
(2)令-x2+2x+3=0,解得x1= -1,x2="3"
∴B(3,0)
设直线BC的解析式为y=kx+b′,则 解得:
解得:
∴直线BC的解析式为y=-x+3
(3)设P(a,3-a),则D(a,-a2+2a+3)
∴PD=(-a2+2a+3)-(3-a)=-a2+3a (7分)
∴



∴当 时,△BDC的面积最大值是
时,△BDC的面积最大值是
考点:一次函数二次函数等
点评:本题难度较大,主要考查学生对函数知识点及图像性质的掌握。为中考常考题型,要求学生培养数形结合思想多做训练,并灵活运用到考试中去。

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
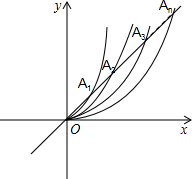 如图,直线y=x与抛物线y=ax2(a>0)在y轴右侧依次交于A1,A2,A3…An,且OA1=A1A2=A2A3=…=An-1An(n为正整数),其中经过点A1的抛物线为y=x2,则过点An的抛物线为( )
如图,直线y=x与抛物线y=ax2(a>0)在y轴右侧依次交于A1,A2,A3…An,且OA1=A1A2=A2A3=…=An-1An(n为正整数),其中经过点A1的抛物线为y=x2,则过点An的抛物线为( )