题目内容
 定义:把一个半圆与抛物线的一部分合成封闭图形,我们把这个封闭图形称为“蛋圆”.如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,8),AB为半圆的直径,半圆的圆心M的坐标为(1,0),半圆半径为3.
定义:把一个半圆与抛物线的一部分合成封闭图形,我们把这个封闭图形称为“蛋圆”.如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,8),AB为半圆的直径,半圆的圆心M的坐标为(1,0),半圆半径为3.(1)请你直接写出“蛋圆”抛物线部分的解析式y
(2)请你求出过点C的“蛋圆”切线与x轴的交点坐标;
(3)求经过点D的“蛋圆”切线的解析式.
考点:二次函数综合题
专题:压轴题
分析:(1)根据半圆的对称性求出点A、B的坐标,然后利用待定系数法求二次函数解析式解答,再根据点A、B的坐标写出x的取值范围;
(2)设过点C的切线与x轴相交于E,连接CM,根据同角的余角相等求出∠CEO=∠MCO,然后根据两组角对应相等,两三角形相似求出△COE和△MOC相似,利用相似三角形对应边成比例求出OE,然后写出点E的坐标即可;
(3)设过点D的“蛋圆”切线解析式为y=kx+8,与抛物线解析式联立,消掉未知数y得到关于x的一元二次方程,再根据相切只有一个交点△=0列式求解即可.
(2)设过点C的切线与x轴相交于E,连接CM,根据同角的余角相等求出∠CEO=∠MCO,然后根据两组角对应相等,两三角形相似求出△COE和△MOC相似,利用相似三角形对应边成比例求出OE,然后写出点E的坐标即可;
(3)设过点D的“蛋圆”切线解析式为y=kx+8,与抛物线解析式联立,消掉未知数y得到关于x的一元二次方程,再根据相切只有一个交点△=0列式求解即可.
解答:解:(1)∵半圆的圆心M的坐标为(1,0),半圆半径为3,
∴A(-2,0),B(4,0),
设抛物线解析式为y=ax2+bx+c,
则
,
解得
,
∴“蛋圆”抛物线部分的解析式y=-x2+2x+8(-2≤x≤4);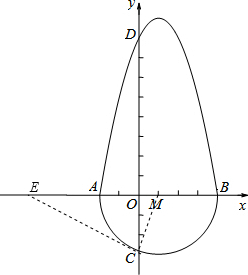
故答案为:=-x2+2x+8;-2≤x≤4.
(2)如图,设过点C的切线与x轴相交于E,连接CM,
∵CE与半圆相切,
∴CE⊥CM,
∴∠OCE+∠MCO=90°,
∵∠CEO+∠ECO=90°,
∴∠CEO=∠MCO,
又∵∠COE=∠MOC=90°,
∴△COE∽△MOC,
∴
=
,
由勾股定理得,OC=
=2
,
∴OE=
=
=8,
∴过点C的“蛋圆”切线与x轴的交点坐标为(-8,0);
(3)设过点D的“蛋圆”切线解析式为y=kx+8,
联立
,
消掉y得,x2+(k-2)x=0,
∵直线与“蛋圆”抛物线相切,
∴△=(k-2)2=0,
解得k=2,
∴过点D的“蛋圆”切线的解析式为y=2x+8.
∴A(-2,0),B(4,0),
设抛物线解析式为y=ax2+bx+c,
则
|
解得
|
∴“蛋圆”抛物线部分的解析式y=-x2+2x+8(-2≤x≤4);

故答案为:=-x2+2x+8;-2≤x≤4.
(2)如图,设过点C的切线与x轴相交于E,连接CM,
∵CE与半圆相切,
∴CE⊥CM,
∴∠OCE+∠MCO=90°,
∵∠CEO+∠ECO=90°,
∴∠CEO=∠MCO,
又∵∠COE=∠MOC=90°,
∴△COE∽△MOC,
∴
| OE |
| OC |
| OC |
| OM |
由勾股定理得,OC=
| 32-12 |
| 2 |
∴OE=
| OC2 |
| OM |
(2
| ||
| 1 |
∴过点C的“蛋圆”切线与x轴的交点坐标为(-8,0);
(3)设过点D的“蛋圆”切线解析式为y=kx+8,
联立
|
消掉y得,x2+(k-2)x=0,
∵直线与“蛋圆”抛物线相切,
∴△=(k-2)2=0,
解得k=2,
∴过点D的“蛋圆”切线的解析式为y=2x+8.
点评:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,相似三角形的判定与性质,切线的定义,读懂题目信息,理解“蛋圆”的定义是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知两圆的圆心距为8cm,半径分别为3cm,5cm,则这两圆的位置关系是( )
| A、内含 | B、内切 | C、相交 | D、外切 |
数轴是一条( )
| A、射线 | B、直线 |
| C、线段 | D、以上都是 |
 幼儿园购买了一个板长AB 4m,支架OC高0.8m的翘翘板,支点O在板AB的中点.因支架过高不宜小朋友玩,故把它暂时存放在高2.4m的车库里,准备改装.现有几个小朋友把板的一端A按到地面上.
幼儿园购买了一个板长AB 4m,支架OC高0.8m的翘翘板,支点O在板AB的中点.因支架过高不宜小朋友玩,故把它暂时存放在高2.4m的车库里,准备改装.现有几个小朋友把板的一端A按到地面上.