题目内容
10.根据等式和不等式的基本性质,我们可以得到比较两数大小的方法:若A-B>0,则A>B,若A-B=0,则A=B,若A-B<0,则A<B,这种比较大小的方法称作“作差法”,请运用这种方法尝试解决下列问题(1)比较3a2-2b+1与5+3a2-2b+b2的大小;
(2)比较a+b与a-b的大小;
(3)比较3a+2b与2a+3b的大小.
分析 (1)、(2)、(3)根据题意列出整式相减的式子,再去括号,合并同类项即可求解.
解答 解:(1)∵(3a2-2b+1)-(5+3a2-2b+b2)
=3a2-2b+1-5-3a2+2b-b2
=-4-b2,
∵b2≥0,
∴-b2≤0,
∴-4-b2<0,
∵3a2-2b+1<5+3a2-2b+b2;
(2)∵(a+b)-(a-b)
=a+b-a+b
=2b,
∴当b>0时,a+b>a-b;
当b=0时,a+b=a-b;
当b<0时,a+b<a-b.
(3)∵(3a+2b)-(2a+3b)
=3a+2b-2a-3b
=a-b,
∴当a>b时,3a+2b>2a+3b;
当a=b时,3a+2b=2a+3b;
当a<b时,3a+2b<2a+3b.
点评 本题考查的是整式的加减,在解答此题时要注意分类讨论思想的灵活应用.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
2.某个体户经营香蕉,7月8日晚库存香蕉0千克,若进价是2.5元/千克.售价是3.3元/千克,7月9日至7月11日这三天销售情况如下表:
(1)第一天结束库存香蕉4千克,第二天结束库存香蕉1千克.
(2)①成本:购进量×进价=375.
②售出额:售出量×售价=452.1.
③损耗费用:损耗量×进价=22.5.
④库存费用:库存量×进价=22.5.
该个体户盈利了吗?请通过分析计算作答.
| 9日 | 10日 | 11日 | |
| 购进(千克) | 50 | 48 | 52 |
| 售出(千克) | 42 | 49 | 46 |
| 损耗(千克) | 4 | 2 | 3 |
(2)①成本:购进量×进价=375.
②售出额:售出量×售价=452.1.
③损耗费用:损耗量×进价=22.5.
④库存费用:库存量×进价=22.5.
该个体户盈利了吗?请通过分析计算作答.

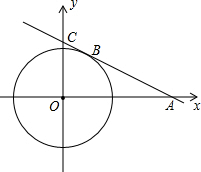 如图,直线y=-$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$交坐标轴于A、C两点,且半径为1的⊙O有公共点B,问:
如图,直线y=-$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$交坐标轴于A、C两点,且半径为1的⊙O有公共点B,问: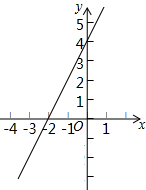 如图所示,直线l是一次函数的图象.
如图所示,直线l是一次函数的图象.