题目内容
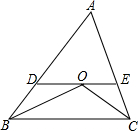 如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.
如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.(1)若AB=7,AC=5,求△ADE的周长;
(2)若∠ABC=∠ACB,AC=10,直接写出图中所有的等腰三角形并求△ADE的周长.
考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:(1)根据角平分线定义和平行线性质求出∴∠DOB=∠DBO,∠EOC=∠ECO,推出OD=DB,OE=EC,即可求出△ADE的周长=AD+AE+DE=AD+DO+OE+AE=AD+DB+AE+EC=AB+AC=12;
(2)根据等角对等边,求得AB=AC=10,由(1)得△ADE的周长=AB+AC即可求得.
(2)根据等角对等边,求得AB=AC=10,由(1)得△ADE的周长=AB+AC即可求得.
解答:解:(1)∵BO平分∠ABC,CO平分∠ACB
∴∠DBO=∠OBC,∠ECO=∠OCB,
∵DE∥BC
∴∠DOB=∠OBC,∠EOC=∠OCB
∴∠DOB=∠DBO,∠EOC=∠ECO,
∴OD=DB,OE=EC,
∵AB=7,AC=5
∴△ADE的周长=AD+AE+DE=AD+DO+OE+AE=AD+DB+AE+EC=AB+AC=12,
(2)图中等腰三角形的有:△ADE,△DBO,△EOC,△OBC,△ABC,
∵∠ABC=∠ACB,AC=10
∴AB=AC=10,
由(1)得△ADE的周长=AB+AC=20.
∴∠DBO=∠OBC,∠ECO=∠OCB,
∵DE∥BC
∴∠DOB=∠OBC,∠EOC=∠OCB
∴∠DOB=∠DBO,∠EOC=∠ECO,
∴OD=DB,OE=EC,
∵AB=7,AC=5
∴△ADE的周长=AD+AE+DE=AD+DO+OE+AE=AD+DB+AE+EC=AB+AC=12,
(2)图中等腰三角形的有:△ADE,△DBO,△EOC,△OBC,△ABC,
∵∠ABC=∠ACB,AC=10
∴AB=AC=10,
由(1)得△ADE的周长=AB+AC=20.
点评:本题考查了角平分线定义,平行线性质,等腰三角形的判定的应用,有效的进行线段的等量代换是正确解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在实数π,
,
,-3.14,
,
中,无理数有( )
| 1 |
| 3 |
| 3 | 27 |
| 4 |
| (-4)2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )
如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )| A、两点确定一条直线 |
| B、两点确定一条线段 |
| C、两点之间,直线最短 |
| D、两点之间,线段最短 |
为了了解某路口每天在学校放学时段的车流量,有下面几个样本统计该路口在学校放学时段的车流量,样本选取合适的是( )
| A、春夏秋冬每个季节各选两周作为样本 |
| B、以全年每一天为样本 |
| C、选取每周星期日为样本 |
| D、抽取两天作为一个样本 |
 如图所示,∠AOB=α,∠AOB内有一点P,在∠AOB的两边上有两个动点Q、R(均不同于点O),现在把△PQR周长最小时∠QPR的度数记为β,则α与β应该满足关系是
如图所示,∠AOB=α,∠AOB内有一点P,在∠AOB的两边上有两个动点Q、R(均不同于点O),现在把△PQR周长最小时∠QPR的度数记为β,则α与β应该满足关系是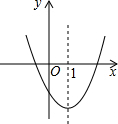 如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1,
如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1,