题目内容
 如图,点A是半径为3的⊙O内一定点,已知OA=
如图,点A是半径为3的⊙O内一定点,已知OA= ,P为⊙O上一点,当∠OPA取最大值时,则sin∠OPA=
,P为⊙O上一点,当∠OPA取最大值时,则sin∠OPA=
- A.

- B.

- C.

- D.

D
分析:作OH⊥PA于H,根据正弦的定义得到sin∠OPA= ,由于OP=3,则当OH最大时,即OH=OA=
,由于OP=3,则当OH最大时,即OH=OA= 时,∠OPA最大,所以sin∠OPA=
时,∠OPA最大,所以sin∠OPA= =
= .
.
解答:作OH⊥PA于H,如图,
∵sin∠OPA= ,
,
∵OP=3,
∴当OH最大时,即OH=OA= 时,∠OPA最大,sin∠OPA最大,
时,∠OPA最大,sin∠OPA最大,
此时sin∠OPA= =
= .
.
故选D.
点评:本题考查了垂径定理:垂直于弦的直径平分弦,且平分弦所对的弧.也考查了锐角三角函数.
分析:作OH⊥PA于H,根据正弦的定义得到sin∠OPA=
 ,由于OP=3,则当OH最大时,即OH=OA=
,由于OP=3,则当OH最大时,即OH=OA= 时,∠OPA最大,所以sin∠OPA=
时,∠OPA最大,所以sin∠OPA= =
= .
.解答:作OH⊥PA于H,如图,

∵sin∠OPA=
 ,
,∵OP=3,
∴当OH最大时,即OH=OA=
 时,∠OPA最大,sin∠OPA最大,
时,∠OPA最大,sin∠OPA最大,此时sin∠OPA=
 =
= .
.故选D.
点评:本题考查了垂径定理:垂直于弦的直径平分弦,且平分弦所对的弧.也考查了锐角三角函数.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
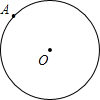 如图,点A是半径为
如图,点A是半径为| 8 |
| π |
A、当P,Q两点运动到1秒时,弦长PQ=
| ||||
B、当点P第一次回到出发点A时所用时间为
| ||||
| C、当P,Q两点从开始运动到第一次成为最大弦时,所用的时间为2秒 | ||||
D、当P,Q两点从开始运动到第一次成为最大弦时,过点A作⊙O的切线与PQ的延长交于M,则MA长为
|
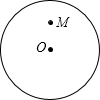 如图,点M是半径为5的⊙O内一点,且OM=3,在过点M的所有⊙O的弦中,弦长为偶数的弦的条数为( )
如图,点M是半径为5的⊙O内一点,且OM=3,在过点M的所有⊙O的弦中,弦长为偶数的弦的条数为( )| A、2 | B、3 | C、4 | D、5 |
 点作⊙O的割线PAB(PB>PA).设PA=x,PB=y.
点作⊙O的割线PAB(PB>PA).设PA=x,PB=y. 8、如图,点P是半径为5的⊙O内一点,且OP=3.过点P任作一条弦AB,则弦AB的长不可能为( )
8、如图,点P是半径为5的⊙O内一点,且OP=3.过点P任作一条弦AB,则弦AB的长不可能为( )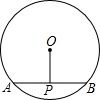 如图,点P是半径为5的⊙O内一点,且弦AB⊥OP,OP=3,则弦AB长是
如图,点P是半径为5的⊙O内一点,且弦AB⊥OP,OP=3,则弦AB长是