题目内容
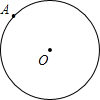 如图,点A是半径为
如图,点A是半径为| 8 |
| π |
A、当P,Q两点运动到1秒时,弦长PQ=
| ||||
B、当点P第一次回到出发点A时所用时间为
| ||||
| C、当P,Q两点从开始运动到第一次成为最大弦时,所用的时间为2秒 | ||||
D、当P,Q两点从开始运动到第一次成为最大弦时,过点A作⊙O的切线与PQ的延长交于M,则MA长为
|
分析:本题关键是利用了弧长公式计算.
解答:解:A、当P,Q两点运动到1秒时,弧PQ=(1+3)×1=4cm,弧PQ对的圆心角为n,则有4=
,∴n=90°,∴弦长PQ=
cm,故A正确;
B、圆的周长=2π×
=16,∴当点P第一次回到出发点A时所用时间=16÷3=
秒,故B正确;
C、当P,Q两点从开始运动到第一次成为最大弦时,最大弦为直径,所用的时间=8÷(1+3)=2秒,故C正确;
D、此时弧AQ=1×2=
,∴弧AQ的度数=45°,即△AMO为等腰直角三角形,有MA=OA=
cm,故D错误.
故选D.
nπ×
| ||
| 180 |
| 8 |
| π |
| 2 |
B、圆的周长=2π×
| 8 |
| π |
| 16 |
| 3 |
C、当P,Q两点从开始运动到第一次成为最大弦时,最大弦为直径,所用的时间=8÷(1+3)=2秒,故C正确;
D、此时弧AQ=1×2=
nπ×
| ||
| 180 |
| 8 |
| π |
故选D.
点评:本题利用了弧长=速度×时间,弧长公式求解.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
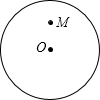 如图,点M是半径为5的⊙O内一点,且OM=3,在过点M的所有⊙O的弦中,弦长为偶数的弦的条数为( )
如图,点M是半径为5的⊙O内一点,且OM=3,在过点M的所有⊙O的弦中,弦长为偶数的弦的条数为( )| A、2 | B、3 | C、4 | D、5 |
 点作⊙O的割线PAB(PB>PA).设PA=x,PB=y.
点作⊙O的割线PAB(PB>PA).设PA=x,PB=y. 8、如图,点P是半径为5的⊙O内一点,且OP=3.过点P任作一条弦AB,则弦AB的长不可能为( )
8、如图,点P是半径为5的⊙O内一点,且OP=3.过点P任作一条弦AB,则弦AB的长不可能为( )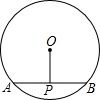 如图,点P是半径为5的⊙O内一点,且弦AB⊥OP,OP=3,则弦AB长是
如图,点P是半径为5的⊙O内一点,且弦AB⊥OP,OP=3,则弦AB长是