题目内容
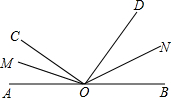 如图所示,如果∠AOB是平角,∠AOC=30°,∠BOD=60°,OM、ON分别是∠AOC、∠BOD的平分线,那么:
如图所示,如果∠AOB是平角,∠AOC=30°,∠BOD=60°,OM、ON分别是∠AOC、∠BOD的平分线,那么:(1)∠MOC=
15°
15°
;(2)∠DON=
30°
30°
;(3)∠COD=
90°
90°
;(4)∠MON=
135°
135°
;(5)∠AOM+∠BON=
45°
45°
.分析:(1)、(2)直接根据角平分线的定义得出结论;
(3)根据∠COD=∠AOB-∠AOC-∠BOD得出结论;
(4)根据∠MON=∠MOC+∠COD+∠DON得出结论;
(5)先根据角平分线的定义得出∠AOM与∠BON的度数,故可得出结论.
(3)根据∠COD=∠AOB-∠AOC-∠BOD得出结论;
(4)根据∠MON=∠MOC+∠COD+∠DON得出结论;
(5)先根据角平分线的定义得出∠AOM与∠BON的度数,故可得出结论.
解答:解:(1)∵∠AOC=30°,OM是∠AOC的平分线,
∴∠MOC=
∠AOC=
×30°=15°.
(2)∵∠BOD=60°,ON是∠BOD的平分线,
∴∠DON=
∠BOD=
×60°=30°.
(3)∵∠AOB是平角,∠AOC=30°,∠BOD=60°,
∴∠COD=∠AOB-∠AOC-∠BOD=180°-30°-60°=90°.
(4)∵∠MOC=15°,∠COD=90°,∠DON=30°,
∴∠MON=∠MOC+∠COD+∠DON=15°+90°+30°=135°.
(5)∵∠AOC=30°,∠BOD=60°,OM、ON分别是∠AOC、∠BOD的平分线,
∴∠AOM=
∠AOC=15°,∠BON=
∠BOD=30°,
∴∠AOM+∠BON=15°+30°=45°.
故答案为:15°;30°;90°;135°;45°.
∴∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |

(2)∵∠BOD=60°,ON是∠BOD的平分线,
∴∠DON=
| 1 |
| 2 |
| 1 |
| 2 |
(3)∵∠AOB是平角,∠AOC=30°,∠BOD=60°,
∴∠COD=∠AOB-∠AOC-∠BOD=180°-30°-60°=90°.
(4)∵∠MOC=15°,∠COD=90°,∠DON=30°,
∴∠MON=∠MOC+∠COD+∠DON=15°+90°+30°=135°.
(5)∵∠AOC=30°,∠BOD=60°,OM、ON分别是∠AOC、∠BOD的平分线,
∴∠AOM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AOM+∠BON=15°+30°=45°.
故答案为:15°;30°;90°;135°;45°.
点评:本题考查的是角平分线的定义,即从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.

练习册系列答案
相关题目
 2008年7月某地区遭受严重的自然灾害,空军某部队奉命赴灾区空投物资,已知空投物资离开飞机后在空中沿抛物线降落,抛物线顶点为机舱舱口A.如图所示.如果空投物资离开A处后下落的垂直高度AB=160米,它到A处的水平距离BC=200米,那么要使飞机在垂直高度AO=1000米的高度进行空投,物资恰好准确地落在居民点P处,飞机到P处的水平距离OP应为多少米
2008年7月某地区遭受严重的自然灾害,空军某部队奉命赴灾区空投物资,已知空投物资离开飞机后在空中沿抛物线降落,抛物线顶点为机舱舱口A.如图所示.如果空投物资离开A处后下落的垂直高度AB=160米,它到A处的水平距离BC=200米,那么要使飞机在垂直高度AO=1000米的高度进行空投,物资恰好准确地落在居民点P处,飞机到P处的水平距离OP应为多少米 一架长为2.5m的梯子,斜靠在竖直的墙上,这时梯子的底端距离墙底AO=0.7m.如图所示.如果梯子底端沿墙下滑0.4m,
一架长为2.5m的梯子,斜靠在竖直的墙上,这时梯子的底端距离墙底AO=0.7m.如图所示.如果梯子底端沿墙下滑0.4m,
 一架长为2.5m的梯子,斜靠在竖直的墙上,这时梯子的底端距离墙底AO=0.7m.如图所示.如果梯子底端沿墙下滑0.4m,
一架长为2.5m的梯子,斜靠在竖直的墙上,这时梯子的底端距离墙底AO=0.7m.如图所示.如果梯子底端沿墙下滑0.4m,