题目内容
已知a,b,c是非零有理数,且满足 ,则
,则 等于________.
等于________.
-
分析:先在等式 两边同乘非零数a,得到a2b2=c-ab,移项得出a2b2-c=-ab,c-a2b2=ab.再将得到的三个等式代入所求代数式,然后化简,即可得出结果.
两边同乘非零数a,得到a2b2=c-ab,移项得出a2b2-c=-ab,c-a2b2=ab.再将得到的三个等式代入所求代数式,然后化简,即可得出结果.
解答:∵ ,
,
∴a2b2=c-ab,a2b2-c=-ab,c-a2b2=ab.
∴ +
+ -
- =(
=( )2+
)2+ -
- =(
=( )2+
)2+ =(
=( )2+
)2+ =
=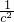 -
- =-
=-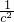 ,
,
 =
= =
= =
=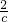 ,
,
 =-
=-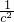 ÷
÷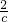 ÷
÷ =-
=-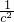 •
• •
• =-
=- .
.
故答案为- .
.
点评:本题考查了分式的化简求值,属于竞赛题型,难度较大.将已知等式变形是关键,将所求代数式分项组合使之能够应用已知条件是难点.

分析:先在等式
 两边同乘非零数a,得到a2b2=c-ab,移项得出a2b2-c=-ab,c-a2b2=ab.再将得到的三个等式代入所求代数式,然后化简,即可得出结果.
两边同乘非零数a,得到a2b2=c-ab,移项得出a2b2-c=-ab,c-a2b2=ab.再将得到的三个等式代入所求代数式,然后化简,即可得出结果.解答:∵
 ,
,∴a2b2=c-ab,a2b2-c=-ab,c-a2b2=ab.
∴
 +
+ -
- =(
=( )2+
)2+ -
- =(
=( )2+
)2+ =(
=( )2+
)2+ =
=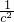 -
- =-
=-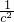 ,
, =
= =
= =
=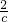 ,
, =-
=-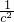 ÷
÷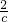 ÷
÷ =-
=-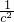 •
• •
• =-
=- .
.故答案为-
 .
.点评:本题考查了分式的化简求值,属于竞赛题型,难度较大.将已知等式变形是关键,将所求代数式分项组合使之能够应用已知条件是难点.

练习册系列答案
相关题目