题目内容
12.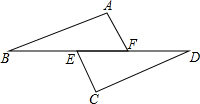 如图,已知AB=CD,AB∥CD,BE=FD,那么AF与CE相等吗?请说明理由.
如图,已知AB=CD,AB∥CD,BE=FD,那么AF与CE相等吗?请说明理由.
分析 根据平行线性质得出∠B=∠D,求出BF=DE,根据SAS证出△ABF≌△CDE即可.
解答 解:AF=CE.
∵AB∥CD,
∴∠B=∠D,
∵BE=FD,
∴BF=DE,
在△ABF和△CDE中
$\left\{\begin{array}{l}{AB=CD}\\{∠B=∠D}\\{BF=DE}\end{array}\right.$
∴△ABF≌△CDE,
∴AF=CE.
点评 本题考查了全等三角形的性质和判定的应用,注意:①全等三角形的对应角相等,对应边相等,②全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
相关题目
2.下列说法正确的是( )
| A. | 同位角相等 | |
| B. | 对顶角相等 | |
| C. | 两条直线被第三条直线所截,内错角相等 | |
| D. | 两条平行直线被第三条直线所截,同旁内角相等 |
3.下列命题中正确的是( )
| A. | 全等三角形的高相等 | B. | 全等三角形的中线相等 | ||
| C. | 全等三角形的角平分线相等 | D. | 全等三角形对应角相等 |
20.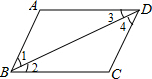 如图,有下列说法:
如图,有下列说法:
①若AD∥BC,∠1=∠3,则BD是∠ABC的平分线;
②若AD∥BC,则∠1=∠4;
③若∠A=∠C,则AB∥CD;
④若∠C+∠3+∠4=180°,则AD∥BC.
其中正确的个数有( )
 如图,有下列说法:
如图,有下列说法:①若AD∥BC,∠1=∠3,则BD是∠ABC的平分线;
②若AD∥BC,则∠1=∠4;
③若∠A=∠C,则AB∥CD;
④若∠C+∠3+∠4=180°,则AD∥BC.
其中正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.化简:$\sqrt{-\frac{1}{a}}$=( )
| A. | $\frac{1}{a}$$\sqrt{a}$ | B. | $\frac{1}{a}$$\sqrt{-a}$ | C. | -$\frac{1}{a}$$\sqrt{-a}$ | D. | -$\frac{1}{a}$$\sqrt{a}$ |
2.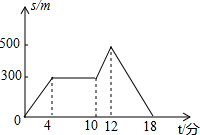 星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s(米)与散步所用时间t(分)之间的关系.依据图象,下面描述符合小红散步情景的是( )
星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s(米)与散步所用时间t(分)之间的关系.依据图象,下面描述符合小红散步情景的是( )
 星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s(米)与散步所用时间t(分)之间的关系.依据图象,下面描述符合小红散步情景的是( )
星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s(米)与散步所用时间t(分)之间的关系.依据图象,下面描述符合小红散步情景的是( )| A. | 从家出发,到了一个公共阅报栏,看了一会儿报,就回家了 | |
| B. | 从家出发,到了一个公共阅报栏,看了一会儿报后,继续向前走了一段,然后回家了 | |
| C. | 从家出发,一直散步(没有停留),然后回家了 | |
| D. | 从家出发,散了一会儿步,就找同学去了,18min后才开始返回 |
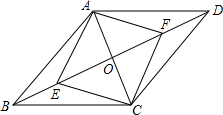 如图,在平行四边形ABCD中,AC、BD相交于点O,点E、F分别是OB、OD的中点.判断四边形AECF的形状并说明理由.
如图,在平行四边形ABCD中,AC、BD相交于点O,点E、F分别是OB、OD的中点.判断四边形AECF的形状并说明理由.