Question

6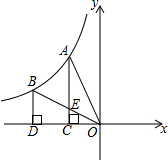．如图，反比例函数y=$\frac{k}{x}$（k≠0）的图象经过A，B两点，过点A作AC⊥x轴，垂足为C，过点B作BD⊥x轴，垂足为D，连接AO，连接BO交AC于点E，若OC=CD，四边形BDCE的面积为2，则k的值为-$\frac{16}{3}$．

Answer 1

分析 先设点B坐标为（a，b），根据平行线分线段成比例定理，求得梯形BDCE的上下底边长与高，再根据四边形BDCE的面积求得ab的值，最后计算k的值．

解答 解：设点B坐标为（a，b），则DO=-a，BD=b
∵AC⊥x轴，BD⊥x轴
∴BD∥AC
∵OC=CD
∴CE=$\frac{1}{2}$BD=$\frac{1}{2}$b，CD=$\frac{1}{2}$DO=$-\frac{1}{2}$a
∵四边形BDCE的面积为2
∴$\frac{1}{2}$（BD+CE）×CD=2，即$\frac{1}{2}$（b+$\frac{1}{2}$b）×（-$\frac{1}{2}$a）=2
∴ab=-$\frac{16}{3}$
将B（a，b）代入反比例函数y=$\frac{k}{x}$（k≠0），得
k=ab=-$\frac{16}{3}$
故答案为：-$\frac{16}{3}$

点评 本题主要考查了反比例函数系数k的几何意义，解决问题的关键是运用数形结合的思想方法进行求解．本题也可以根据△OCE与△ODB相似比为1：2求得△BOD的面积，进而得到k的值．