Question

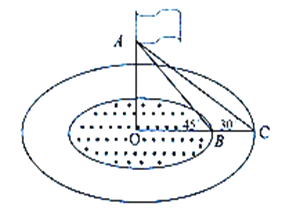
【题目】如图，学校旗杆的下方有一块圆形草坪，草坪的外面围着“圆环”水池，草坪和水池的外边缘是两个同心圆，旗杆在圆心O的位置且与地面垂直.

（1）若草坪的面积与圆环水池的面积之比为1∶4，求两个同心圆的半径之比.

（2）如图，若水池外面通往草坪有一座10米长的小桥BC，小桥所在的直线经过圆心O，上午8:00时太阳光线与地面成30°角，旗杆顶端的影子恰好落在水池的外缘；上午9:00时太阳光线与地面成45°角，旗杆顶端的影子恰好落在草坪的外缘，求旗杆的高OA长.

Answer 1

【答案】（1）；（2）旗杆的高OA长为（）米.

【解析】

（1）根据面积比与半径比的关系求解即；

（2）设OA=x，根据解直角三角形表示出OB，OC，根据其数量关系列方程解答即可.

（1）由题意得，

∴，

即两个同心圆的半径之比为.

（2）设OA=x，由∠ABO=45°，∠ACO=30°知，

，

，

∵，OC-OB=BC=10

∴，解得.

∴旗杆的高OA长为（）米.