题目内容
17．如图在Rt△ABC中，∠C=90°，AC=4，BC=3，在Rt△ABC的外部拼接一个合适的直角三角形，使得拼接后的三角形是一个等腰三角形．要求：要求在备用的图中分别画出四种与图例不同的拼接方法，在图中标明拼接的直角三角形的三边长．
分析 根据勾股定理可以求得直角三角形的斜边长，构成等腰三角形，则根据原直角三角形斜边长和直角边长可以确定另一个直角三角形的一条直角边长，根据这个等量关系可以解题．
解答 解：在Rt△ABC中，∠C=90°，AC=4，BC=3，则AB=5．
如图所示：
．
点评 本题考查了等腰三角形腰长相等的性质，本题中根据斜边分别求新直角三角形的直角边长是解题的关键．
练习册系列答案
相关题目
9．
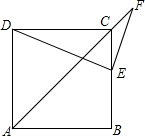如图，正方形ABCD的边长为10+5$\sqrt{2}$，点E在边CB上，点F在AC的延长线上，EF⊥DE．若CE=CF，则CE的值为（ ）
如图，正方形ABCD的边长为10+5$\sqrt{2}$，点E在边CB上，点F在AC的延长线上，EF⊥DE．若CE=CF，则CE的值为（ ）| A． | 5 | B． | 5$\sqrt{2}$ | C． | 10 | D． | 10$\sqrt{2}$ |