题目内容
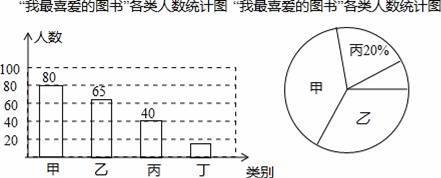
某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
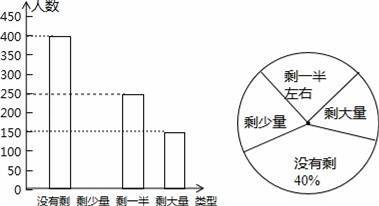

(1)这次被调查的同学共有 名;“剩大量”的扇形圆心角是 .
(2)把条形统计图补充完整;
(3)在被调查的学生中随机抽取一名恰巧是“剩少量”或“剩一半左右”饭的概率多大;
(4)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐?
【考点】条形统计图;用样本估计总体;扇形统计图;概率公式.
【分析】(1)根据“没有剩”的人数除以“没有剩”的人数所占的百分比,可得调查的人数,根据“剩大量”的人数除以调查的人数乘以360°,可得答案;
(2)根据有理数的减法,可得“剩少量”的人数,根据“剩少量”的人数,可得答案;
(3)根据“剩少量”的人数与“剩一半”的人数的和除以调查的人数,可得答案;
(4)根据总人数乘以“食用一餐的人数与调查的人数比”,可得答案.
【解答】解:(1)这次被调查的同学共有400÷40%=1000人;
“剩大量”的扇形圆心角是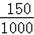
 ×360°=54°,
×360°=54°,
故答案为:1000,54°;
(2)“剩少量”的人数1000﹣400﹣250﹣150=200人,
补充完整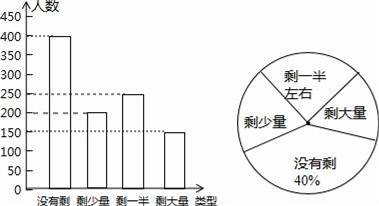
 ;
;
(3)在被调查的学生中随机抽取一名恰巧是“剩少量”或“剩一半左右”饭的概率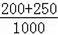
 =
=
 ;
;
(4)学生一餐浪费的食物可供18000×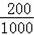
 =3600人食用一餐.
=3600人食用一餐.

练习册系列答案
相关题目

 ,把它的解集在数轴上表示出来,并求出这个不等式的负整数解.
,把它的解集在数轴上表示出来,并求出这个不等式的负整数解.
 B.
B.

 D.
D.


 ÷
÷



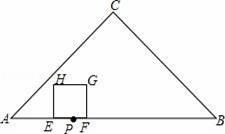
 的图象如图所示 ,则函数
的图象如图所示 ,则函数 的图像是( )
的图像是( )
