Question

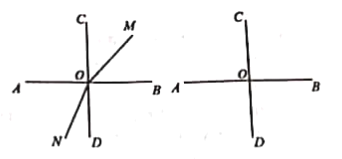
【题目】如图，两条直线AB,CD相交于点O，且，射线OM从OB开始绕O点逆时针方向旋转，速度为，射线ON同时从OD开始绕O点顺时针方向旋转，速度为.两条射线OM、ON同时运动，运动时间为t秒.（本题出现的角均小于平角）

（1）当时，若.试求出的值；

（2）当时，探究的值，问：t满足怎样的条件是定值；满足怎样的条件不是定值？

Answer 1

【答案】（1）t的值为1秒或秒；

（2）当0＜t＜时，的值是1；当＜t＜6时，不是定值．

【解析】

（1）分两种情况：①如图所示，当0＜t≤7.5时，②如图所示，当7.5＜t＜12时，分别根据已知条件列等式可得t的值；

（2）分两种情况，分别计算∠COM、∠BON和∠MON的度数，代入可得结论．

（1）当ON与OA重合时，t=90÷12=7.5（s）

当OM与OA重合时，t=180°÷15=12（s）

①如图所示，当0＜t≤7.5时，∠AON=90°-12t°，∠AOM=180°-15t°，

由∠AOM=3∠AON-69°，可得180-15t=3（90-12t）-69，

解得t=1；

②如图所示，当7.5＜t＜12时，∠AON=12t°-90°，∠AOM=180°-15t°，

由∠AOM=3∠AON-69°，可得180-15t=3（12t-90）-69，解得t=，

综上，t的值为1秒或秒；

（2）当∠MON=180°时，∠BOM+∠BOD+∠DON=180°，

∴15t+90+12t=180，解得t=，

①如图所示，当0＜t＜时，∠COM=90°-15t°，∠BON=90°+12t°，

∠MON=∠BOM+∠BOD+∠DON=15t°+90°+12t°=，

∴===1（是定值），

②如图所示，当＜t＜6时，∠COM=90°-15t°，∠BON=90°+12t°，

∠MON=360°-/span>（∠BOM+∠BOD+∠DON）=360°-（15t°+90°+12t°）=270°-27t°，

∴==（不是定值），

综上所述，当0＜t＜时，的值是1；当＜t＜6时，不是定值．