题目内容
已知抛物线y=| 1 | 2 |
(1)求k的取值范围;
(2)设抛物线与x轴的一个交点为A(-1,0),求此抛物线的解析式,并求出与x轴的另一个交点B的坐标;
(3)在(2)的条件下,抛物线与y轴交于点C,点D在y轴的正半轴上,且以A、O、D为顶点的三角形和以B、O、C为顶点的三角形相似,求点D的坐标.
分析:(1)根据抛物线与x轴交点个数与相对应的一元二次方程的根的判别式的关系即可解答;
(2)将A(-1,0)代入y=
x2-x+k即可求出k的值,从而得到抛物线的解析式.
(3)根据题意,分△OCB∽△OAD和△OCB∽△ODA两种情况讨论.
(2)将A(-1,0)代入y=
| 1 |
| 2 |
(3)根据题意,分△OCB∽△OAD和△OCB∽△ODA两种情况讨论.
解答: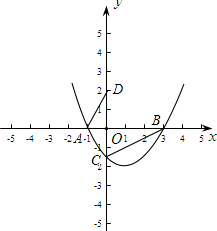 解:(1)∵抛物线y=
解:(1)∵抛物线y=
x2-x+k与x轴有两个交点,
∴△>0,
∴(-1)2-4×
k>0,
∴解得k<
;
(2)将A(-1,0)代入y=
x2-x+k得,
+1+k=0,
解得k=-
,
则函数解析式为y=
x2-x-
.
当y=0时,
x2-x-
=0,
解得x1=-1,x2=3.
于是B点坐标为(3,0);
(3)设点D坐标为(0,y),y>0,
因以A、O、D为顶点的三角形和以B、O、C为顶点的三角形相似,
则①△OCB∽△OAD,
=
,
即
=
,
解得OD=
,故D(0,
);
②△OCB∽△ODA,
=
,
即OD=
,
故点D的坐标为:(0,
)或(0,
).
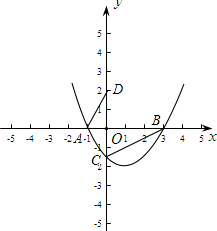 解:(1)∵抛物线y=
解:(1)∵抛物线y=| 1 |
| 2 |
∴△>0,
∴(-1)2-4×
| 1 |
| 2 |
∴解得k<
| 1 |
| 2 |
(2)将A(-1,0)代入y=
| 1 |
| 2 |
| 1 |
| 2 |
解得k=-
| 3 |
| 2 |
则函数解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
当y=0时,
| 1 |
| 2 |
| 3 |
| 2 |
解得x1=-1,x2=3.
于是B点坐标为(3,0);
(3)设点D坐标为(0,y),y>0,
因以A、O、D为顶点的三角形和以B、O、C为顶点的三角形相似,
则①△OCB∽△OAD,
| OC |
| OA |
| OB |
| OD |
即
| 2 |
| 1 |
| 3 |
| OD |
解得OD=
| 3 |
| 2 |
| 3 |
| 2 |
②△OCB∽△ODA,
| OC |
| OB |
| OD |
| OA |
即OD=
| 2 |
| 3 |
故点D的坐标为:(0,
| 3 |
| 2 |
| 2 |
| 3 |
点评:此题考查了二次函数的综合运用,涉及抛物线的性质、相似三角形的性质等内容,要注意分类讨论.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 角形?若存在,求出点P的坐标;若不存在,请说明理由.
角形?若存在,求出点P的坐标;若不存在,请说明理由.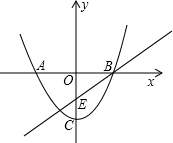 已知抛物线y=ax2+c与x轴交于A、B两点,与y轴交于C点,直线y=
已知抛物线y=ax2+c与x轴交于A、B两点,与y轴交于C点,直线y=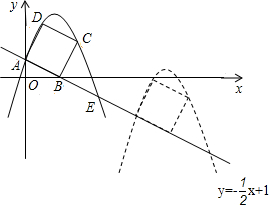
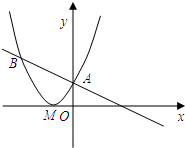
 如图,已知直线
如图,已知直线 +12x-19的顶点的横坐标是3,则a=________.
+12x-19的顶点的横坐标是3,则a=________.