题目内容
抛物线y=-5x2-4x+7与y轴的交点坐标为（ ）
| A、（7，0） |
| B、（-7，0） |
| C、（0，7） |
| D、（0，-7） |
考点：二次函数图象上点的坐标特征
专题：
分析：把x=0代入抛物线y=-5x2-4x+7，即得抛物线y=-5x2-4x+7与y轴的交点．
解答：解：由题意得，当x=0时，抛物线y=-5x2-4x+7与y轴相交，
把x=0代入y=-5x2-4x+7，求得y=7，
所以抛物线y=-5x2-4x+7与y轴的交点坐标为（0，7）．
故选C．
把x=0代入y=-5x2-4x+7，求得y=7，
所以抛物线y=-5x2-4x+7与y轴的交点坐标为（0，7）．
故选C．
点评：本题考查了二次函数图象上点的坐标特征，抛物线与y轴交点的纵坐标是函数解析中的c值．
练习册系列答案
相关题目
代数式
+
+
的所有可能的值有（ ）
| a |
| |a| |
| b |
| |b| |
| ab |
| |ab| |
| A、2个 | B、3个 | C、4个 | D、无数个 |
如图，为二次函数y=ax2+bx+c的图象，在下列说法中：若两圆外切，半径分别为4和7，则它们的圆心距是（ ）
| A、2 | B、3 | C、6 | D、11 |
计算|-
|的结果是（ ）
| 1 |
| 3 |
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
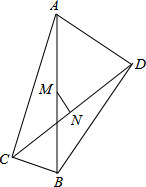在四边形ABCD中，∠ACB=∠ADB=90°，M、N分别是对角线AB、CD的中点，连接MN，MN与CD有怎样的特殊位置关系？证明你的结论．