题目内容
已知△ABC,∠BAC=90°,AB=AC=4,BD是AC边上的中线,分别以AB、AC所在的直线为x轴和y轴建立平面直角 坐标系(如图).
坐标系(如图).
(1)求直线BD的函数关系式;
(2)在BD所在的直线上求一点P,使四边形ABCP为平行四边形(保留作图痕迹),并简要说明作法,根据作图过程,说明作出的四边形是平行四边形;
(3)求出点P的坐标.
 坐标系(如图).
坐标系(如图).(1)求直线BD的函数关系式;
(2)在BD所在的直线上求一点P,使四边形ABCP为平行四边形(保留作图痕迹),并简要说明作法,根据作图过程,说明作出的四边形是平行四边形;
(3)求出点P的坐标.
分析:(1)先求出点D的坐标,然后利用待定系数法即可得出直线BD的函数关系式;
(2)延长BD至P使BD=BP,则点P即是要找的点;
(3)根据平行四边形的性质可得CP∥AB,且CP=AB,从而可得出点P的坐标.
(2)延长BD至P使BD=BP,则点P即是要找的点;
(3)根据平行四边形的性质可得CP∥AB,且CP=AB,从而可得出点P的坐标.
解答: 解:(1)∵AB=AC=4,BD是AC边上的中线,
解:(1)∵AB=AC=4,BD是AC边上的中线,
∴点B坐标为(0,4),点D坐标为(2,0),
设直线BD的函数解析式为:y=kx+b,
则
,
解得:
,
故直线BD的函数关系式为y=-2x+4;
(2)延长BD至P使BD=DP,连接AP、CP,则四边形ABCP为平行四边形.
 由题意得,AD=DC,
由题意得,AD=DC,
又∵BD=DP,
∴四边形ABCP是平行四边形(对角线互相平分的四边形是平行四边形);
(2)∵ABCP是平行四边形,
∴CP
AB,
故可得点P的纵坐标为-4,代入直线BD解析式可得点P的横坐标为4,
即可得点P的坐标为(4,-4).
 解:(1)∵AB=AC=4,BD是AC边上的中线,
解:(1)∵AB=AC=4,BD是AC边上的中线,∴点B坐标为(0,4),点D坐标为(2,0),
设直线BD的函数解析式为:y=kx+b,
则
|
解得:
|
故直线BD的函数关系式为y=-2x+4;
(2)延长BD至P使BD=DP,连接AP、CP,则四边形ABCP为平行四边形.
 由题意得,AD=DC,
由题意得,AD=DC,又∵BD=DP,
∴四边形ABCP是平行四边形(对角线互相平分的四边形是平行四边形);
(2)∵ABCP是平行四边形,
∴CP
| ∥ |
. |
故可得点P的纵坐标为-4,代入直线BD解析式可得点P的横坐标为4,
即可得点P的坐标为(4,-4).
点评:此题考查了一次函数的综合题,解答本题需要求出点D的坐标,从而得出直线BD的函数解析式,第二问需要我们熟练掌握平行四边形的判定定理,难度一般.

练习册系列答案
相关题目
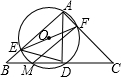 如图,已知△ABC为等腰直角三角形,D为斜边BC的中点,经过点A、D的⊙O与边AB、AC、BC分别相交于点E、F、M.对于如下五个结论:①∠FMC=45°;②AE+AF=AB;③
如图,已知△ABC为等腰直角三角形,D为斜边BC的中点,经过点A、D的⊙O与边AB、AC、BC分别相交于点E、F、M.对于如下五个结论:①∠FMC=45°;②AE+AF=AB;③ 25、如图,已知△ABC为等边三角形,延长BC到D,延长BA到E,并且使AE=BD,连接CE,DE.求证:EC=ED.
25、如图,已知△ABC为等边三角形,延长BC到D,延长BA到E,并且使AE=BD,连接CE,DE.求证:EC=ED. 如图,已知△ABC中,AB=10cm,AC=8cm,BC=6cm,如果点P由B出发沿BA方向向点A匀速运动,速度为2cm/s,同时点Q由A出发沿AC方向向点C匀速运动,速度为1cm/s,连接PQ,设运动的时间为t(单位:s)(0≤t≤5).解答下列问题:
如图,已知△ABC中,AB=10cm,AC=8cm,BC=6cm,如果点P由B出发沿BA方向向点A匀速运动,速度为2cm/s,同时点Q由A出发沿AC方向向点C匀速运动,速度为1cm/s,连接PQ,设运动的时间为t(单位:s)(0≤t≤5).解答下列问题: 22、(1)小方格中△ABC沿BA方向平移,平移的距离为线段AB的2倍;
22、(1)小方格中△ABC沿BA方向平移,平移的距离为线段AB的2倍;