题目内容
在菱形ABCD中,E、F分别是BC和CD的中点,且AE⊥BC,AF⊥CD,那么∠EAF等于
- A.45°
- B.55°
- C.60°
- D.75°
C
分析:连接AC,由题意可得,△ABC是等边三角形从而得到∠EAC=30°,同理可求得∠FAC的度数,从而不难求得∠EAF的度数.
解答: 解:连接AC,
解:连接AC,
由题意可知,△ABC是等边三角形,AE平分∠BAC,所以∠EAC=30°;
同理可得,∠FAC=30°,所以∠EAF=∠EAC+∠FAC=60°.
故选C.
点评:此题主要考查菱形的性质和等边三角形的判定和性质,属于基础题,比较容易解答.
分析:连接AC,由题意可得,△ABC是等边三角形从而得到∠EAC=30°,同理可求得∠FAC的度数,从而不难求得∠EAF的度数.
解答:
 解:连接AC,
解:连接AC,由题意可知,△ABC是等边三角形,AE平分∠BAC,所以∠EAC=30°;
同理可得,∠FAC=30°,所以∠EAF=∠EAC+∠FAC=60°.
故选C.
点评:此题主要考查菱形的性质和等边三角形的判定和性质,属于基础题,比较容易解答.

练习册系列答案
相关题目
 14、如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF的度数=
14、如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF的度数=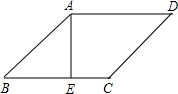 如图,在菱形ABCD中,AE⊥BC于E,已知EC=1,cosB=
如图,在菱形ABCD中,AE⊥BC于E,已知EC=1,cosB= 如图所示,在菱形ABCD中,AC,BD交于点O,AB=15,AO=12,P从A出发,Q从O出发,分别以2cm/s和1cm/s的速度各自向O,B点运动,当运动时间为多少秒时,四边形BQPA的面积是△POQ面积的8倍.
如图所示,在菱形ABCD中,AC,BD交于点O,AB=15,AO=12,P从A出发,Q从O出发,分别以2cm/s和1cm/s的速度各自向O,B点运动,当运动时间为多少秒时,四边形BQPA的面积是△POQ面积的8倍. 如图,在菱形ABCD中,P为对角线BD上一点,连接AP,若AP=BP,AD=PD,则∠PAC的度数是( )
如图,在菱形ABCD中,P为对角线BD上一点,连接AP,若AP=BP,AD=PD,则∠PAC的度数是( )