题目内容
如图,一艘旅游船从A点驶向C点.旅游船先从A点沿以D为圆心的弧AB行驶到B点,然后从B点沿直径行驶到圆D上的C点.假如旅游船在整个行驶过程中保持以每小时40海里的速度行驶,下图2表示旅游船在行驶过程中与点D的距离y和行驶时间t之间的函数图象.根据图中提供的信息,解答下列问题:
(1)在图2中线段MN表示旅游船在 上行驶时与点D的距离y和行驶时间t之间的函数关系图象;图2中折线NHG表示旅游船在 上行驶时与点D的距离y和行驶时间t之间的函数关系图象.
(2)求线段HG表示的函数关系式及自变量t的取值范围.

(1)在图2中线段MN表示旅游船在
(2)求线段HG表示的函数关系式及自变量t的取值范围.

考点:动点问题的函数图象,一次函数的应用
专题:动点型
分析:(1)根据圆上各点到圆心的距离相等判断MN,根据从点B到点D距离逐渐变小,从点D到点C距离逐渐变大解答;
(2)根据图2判断出⊙D的半径,并求出旅游船的速度,然后求出从点B到点D的时间,从而求出点H的坐标,再根据⊙D的半径以及从点D到点C到点时间求出点G的坐标,然后利用待定系数法求一次函数解析式解答即可.
(2)根据图2判断出⊙D的半径,并求出旅游船的速度,然后求出从点B到点D的时间,从而求出点H的坐标,再根据⊙D的半径以及从点D到点C到点时间求出点G的坐标,然后利用待定系数法求一次函数解析式解答即可.
解答:解:(1)由图可知,线段MN表示到点D的距离不变,根据圆的定义,
在弧AB上行驶到点D的距离不变,
从直径BC的点B到点D的行驶过程中,到点D的距离先变小再变大.
故答案为:弧AB,直径BC;
(2)由图可知,⊙D的半径为20海里,
∵旅游船的速度是每小时40海里,
∴从点B到点D和从点D到点C的时间都是20÷40=
小时,
+
=
,
+
=
,
∴点H的坐标为(
,0),点G的坐标为(
,20),
设线段HG的函数关系式为y=kt+b,
则
,
解得
,
所以线段HG表示的函数关系式为y=40t-50(
≤t≤
).
在弧AB上行驶到点D的距离不变,
从直径BC的点B到点D的行驶过程中,到点D的距离先变小再变大.
故答案为:弧AB,直径BC;
(2)由图可知,⊙D的半径为20海里,
∵旅游船的速度是每小时40海里,
∴从点B到点D和从点D到点C的时间都是20÷40=
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
| 1 |
| 2 |
| 7 |
| 4 |
∴点H的坐标为(
| 5 |
| 4 |
| 7 |
| 4 |
设线段HG的函数关系式为y=kt+b,
则
|
解得
|
所以线段HG表示的函数关系式为y=40t-50(
| 5 |
| 4 |
| 7 |
| 4 |
点评:本题考查了动点问题的函数图象,熟练掌握圆上的各点到圆心的距离相等判断出圆的半径是解题的关键.

练习册系列答案
相关题目
下列各式中,与
不是同类根式的是( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如果a=-2+
,那么1+
的值为( )
| 2 |
| 1 | ||
2+
|
A、-
| ||
B、
| ||
| C、2 | ||
D、2
|
下列调查中,适宜采用普查方式的是( )
| A、调查全国中学生的视力情况 |
| B、调查重庆新闻节目”天天630”的收视率 |
| C、调查“神九”航天飞船各零部件的质量 |
| D、调查重庆市民对生活质量的满意程度 |
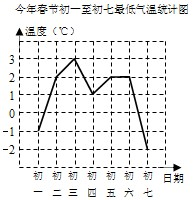 小华同学根据某地今年春节初一至初七的每天最低气温绘成了所示的折线统计图.关于这7天的每天最低气温的说法不正确的是( )
小华同学根据某地今年春节初一至初七的每天最低气温绘成了所示的折线统计图.关于这7天的每天最低气温的说法不正确的是( )| A、极差是5℃ |
| B、众数是2℃ |
| C、中位数是1℃ |
| D、平均数是1℃ |