题目内容
阅读下列解题过程:
为了求1+2+22+23+…+2100的值,可令S=1+2+22+23+…+2100,则2S=2+22+23+24+…+2101,因此2S-S=2101-1,所以S=2101-1,即1+2+22+23+…+2100=2101-1,仿照以上方法计算1+3+32+33+…+32014.
为了求1+2+22+23+…+2100的值,可令S=1+2+22+23+…+2100,则2S=2+22+23+24+…+2101,因此2S-S=2101-1,所以S=2101-1,即1+2+22+23+…+2100=2101-1,仿照以上方法计算1+3+32+33+…+32014.
考点:有理数的乘方
专题:阅读型
分析:利用题中的方法求出原式的值即可.
解答:解:设M=1+3+32+33+…+32014,①
①式两边都乘以3,得3M=3+32+33+…+32015,②
②-①得:2M=32015-1,即M=
,
则原式=
.
①式两边都乘以3,得3M=3+32+33+…+32015,②
②-①得:2M=32015-1,即M=
| 32015-1 |
| 2 |
则原式=
| 32015-1 |
| 2 |
点评:此题考查了有理数的乘方,弄清题中的方法是解本题的关键.

练习册系列答案
相关题目
计算(2x-3y)(4x2+6xy+9y2)的正确结果是( )
| A、(2x-3y)2 |
| B、(2x+3y)2 |
| C、8x3-27y3 |
甲队有32人,乙队有28人,现从乙队抽x人到甲队,使甲队人数是乙队人数的2倍,据题意可列方程为( )
| A、32+x=56 |
| B、32=2(28-x) |
| C、32+x=2(28-x) |
| D、2(32+x)=28-x |
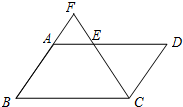 如图,平行四边形ABCD中,E是AD上的点,延长CE交BA的延长线于点F,且AB=AF,请判断AE和DE的大小关系,并请出理由.
如图,平行四边形ABCD中,E是AD上的点,延长CE交BA的延长线于点F,且AB=AF,请判断AE和DE的大小关系,并请出理由.