Question

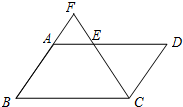如图，平行四边形ABCD中，E是AD上的点，延长CE交BA的延长线于点F，且AB=AF，请判断AE和DE的大小关系，并请出理由．

Answer 1

考点：平行四边形的性质

专题：

分析：由四边形ABCD是平行四边形，可得AB=CD，AB∥CD，又由AB=AF，易证得△AEF≌△DEC，继而证得AE=DE．

解答：解：AE=DE．
理由：∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，
∴∠F=∠ECD，
∵AB=AF，
∴AF=CD，
在△AEF和△DEC中，

∠F=∠DCE ∠AEF=∠DEC AF=CD

，
∴△AEF≌△DEC（AAS），
∴AE=DE．

点评：此题考查了平行四边形的性质以及全等三角形的判定与性质．此题难度不大，注意掌握数形结合思想的应用．