题目内容
17. 是一张直角三角形的纸片.两直角边AC=6cm,BC=8cm将△ABC折叠,使点B与点A重合,折痕为DE,则AD的长为$\frac{25}{4}$cm.
是一张直角三角形的纸片.两直角边AC=6cm,BC=8cm将△ABC折叠,使点B与点A重合,折痕为DE,则AD的长为$\frac{25}{4}$cm.
分析 首先设AD=xcm,由折叠的性质得:BD=AD=xcm,又由BC=8cm,可得CD=8-x(cm),然后在Rt△ACD中,利用勾股定理即可求得方程,解方程即可求得答案.
解答 解:设AD=xcm,
由折叠的性质得:BD=AD=xcm,
∵在Rt△ABC中,AC=6cm,BC=8cm,
∴CD=BC-BD=8-x(cm),
在Rt△ACD中,AC2+CD2=AD2,
即:62+(8-x)2=x2,
解得:x=$\frac{25}{4}$,
∴AD=$\frac{25}{4}$cm.
故答案为:$\frac{25}{4}$cm.
点评 此题考查了折叠的性质与勾股定理的知识.此题难度适中,注意掌握数形结合思想与方程思想的应用,注意掌握折叠前后图形的对应关系.

练习册系列答案
相关题目
5.在下列命题中,正确的是( )
| A. | 正多边形一个内角与一个外角相等,则它是正六边形 | |
| B. | 正多边形都是中心对称图形 | |
| C. | 边数大于3的正多边形的对角线长都相等 | |
| D. | 正多边形的一个外角为36°,则它是正十边形 |
 如图,已知AB=AC,BE=CD,∠B=∠C,则△ABD≌ACE,根据是SAS.
如图,已知AB=AC,BE=CD,∠B=∠C,则△ABD≌ACE,根据是SAS.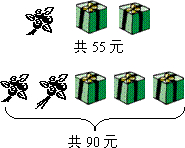 母亲节那天,很多同学给妈妈准备了鲜花和礼盒.
母亲节那天,很多同学给妈妈准备了鲜花和礼盒.