题目内容

11．在△ABC中，AB=AC，∠B=2∠A，则∠A=36°，∠B=72°，∠C=72°．

分析 设∠A=x，则∠B=∠C=2x，再由三角形内角和定理求出x的值即可．

解答 解：∵AB=AC，
∴∠B=∠C，
设∠A=x，则∠B=∠C=2x，
∵∠A+∠B+∠C=180°，
∴x+2x+2x=180°，
解得x=36°，
∴∠A=36°，∠B=72°，∠C=72°，
故答案为：36°，72°，72°．

点评 本题考查的是等腰三角形的性质，三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．

练习册系列答案
相关题目
1．如图，已知抛物线的顶点为M（2，-4），且过点A（-1，5），连结AM交x轴于点B．
（1）求这条抛物线的解析式；
（2）设点P（x，y）是抛物线在x轴下方、顶点 M左方一段上的动点，连结PO，以PO、PQ为腰的等腰三角形的另一顶点Q在x轴上，过Q作x轴的垂线交直线AM于点R，连结PR．设△PQR的面积为S．求S与x之间的函数解析式；
（3）在上述动点P（x，y）中，是否存在使S△PQR=2的点？若存在，求点P的坐标；若不存在，说明理由．
（4）在（3）的条件下，第一象限内的一点N与B，Q组成的三角形与△PQO相似，求N的坐标．
2．已知正比例函数y1=k1x和反比例函数${y_2}=\frac{K_2}{x}$的比例系数k1和k2互为倒数，且正比例函数的图象经过点（2，1）．
（1）求这两个函数解析式．
（2）如果y=y1+y2，求当x=$\sqrt{3}$时，y的值是多少？
19．已知x2-2x-5=0，求3x2-6x-1的值．
6．到三角形三个顶点距离相等的是（　　）
A．两边垂直平分线的交点B．两角平分线的交点
C．两条高的交点D．没有这样的点
16．$\sqrt{x+2}+|{y-2}|=0$，则${（\frac{x}{y}）^{2015}}$=（　　）
A．0B．1C．-1D．2
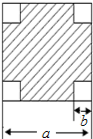3．如图，在一块边长为a厘米的正方形纸板四角，各剪去一个边长为b（b＜$\frac{a}{2}$）厘米的正方形，利用因式分解计算当a=13.4，b=3.4时，剩余部分的面积．
20．下列四个数中，最小的数是（　　）
A．-2B．2C．0D．-1
1．若点（-3，2）在正比例函数y=kx的图象上，则此函数的解析式为y=-$\frac{2}{3}$x．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网