题目内容
3.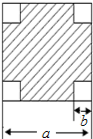 如图,在一块边长为a厘米的正方形纸板四角,各剪去一个边长为b(b<$\frac{a}{2}$)厘米的正方形,利用因式分解计算当a=13.4,b=3.4时,剩余部分的面积.
如图,在一块边长为a厘米的正方形纸板四角,各剪去一个边长为b(b<$\frac{a}{2}$)厘米的正方形,利用因式分解计算当a=13.4,b=3.4时,剩余部分的面积.
分析 根据剩余的面积=大正方形的面积-4个小正方形的面积,由大正方形的边长为a厘米,小正方形的边长为b厘米,利用正方形的面积公式列出剩余部分的面积S,利用平方差公式分解因式后,将a与b的值代入,即可求出剩余部分的面积.
解答 解:根据题意得:剩余部分的面积S=a2-4b2=(a+2b)(a-2b),
当a=13.4,b=3.4时,
原式=(13.4+2×3.4)(13.4-2×2.4)
=20×8.4
=168(平方厘米),
答:当a=13.4,b=3.4时,剩余部分的面积为168平方厘米.
点评 此题考查了因式分解的应用,有时可以利用平方差公式及完全平方公式来简化运算.根据题意列出相应的算式是解本题的关键.

练习册系列答案
相关题目
18.若(x+a)(x+b)的结果中不含有x的一次项,则a、b的关系是( )
| A. | ab=1 | B. | ab=0 | C. | a-b=0 | D. | a+b=0 |
8.若关于x的一元二次方程的两根之和为3,两根之积为2,则这个方程是( )
| A. | x2+3x-2=0 | B. | x2-3x+2=0 | C. | x2-2x+3=0 | D. | x2+3x+2=0 |
13.在代数式xy2中,x与y的值各减少50%,则代数式的值( )
| A. | 减少50% | B. | 减少其值的$\frac{7}{8}$ | C. | 减少其值的$\frac{1}{8}$ | D. | 减少75% |
 如图,已知平行四边形ABCD,E为BC的中点,连接BD交AE为F,△BEF的面积为1,BE=3,则平行四边形ABCD的面积为12.
如图,已知平行四边形ABCD,E为BC的中点,连接BD交AE为F,△BEF的面积为1,BE=3,则平行四边形ABCD的面积为12.