题目内容
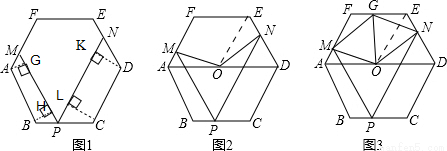
如图1,正六边形ABCDEF的边长为a,P是BC边上一动点,过P作PM∥AB交AF于M,作PN∥CD交DE于N.
(1)①∠MPN= ;
②求证:PM+PN=3a;
(2)如图2,点O是AD的中点,连接OM、ON,求证:OM=ON;
(3)如图3,点O是AD的中点,OG平分∠MON,判断四边形OMGN是否为特殊四边形?并说明理由.

(1)①60°,②证明见解析;
(2)证明见解析;
(3)四边形MONG是菱形,理由见解析.
【解析】
试题分析:(1)①运用∠MPN=180°-∠BPM-∠NPC求解,②作AG⊥MP交MP于点G,BH⊥MP于点H,CL⊥PN于点L,DK⊥PN于点K,利用MP+PN=MG+GH+HP+PL+LK+KN求解,
(2)连接OE,由△OMA≌△ONE证明,
(3)连接OE,由△OMA≌△ONE,再证出△GOE≌△NOD,由△ONG是等边三角形和△MOG是等边三角形求出四边形MONG是菱形.
试题解析:(1)①∵四边形ABCDEF是正六边形,
∴∠A=∠B=∠C=∠D=∠E=∠F=120°.
又∴PM∥AB,PN∥CD,
∴∠BPM=60°,∠NPC=60°,
∴∠MPN=180°-∠BPM-∠NPC=180°-60°-60°=60°,
故答案为;60°.
②如图1,作AG⊥MP交MP于点G,BH⊥MP于点H,CL⊥PN于点L,DK⊥PN于点K,
MP+PN=MG+GH+HP+PL+LK+KN.
∵正六边形ABCDEF中,PM∥AB,作PN∥CD,
∵∠AMG=∠BPH=∠CPL=∠DNK=60°,
∴ ,
,
∵AM=BP,PC=DN,
∴MG+HP+PL+KN=a,GH=LK=a,
∴MP+PN=MG+GH+HP+PL+LK+KN=3a.
(2)如图2,连接OE,
∵四边形ABCDEF是正六边形,AB∥MP,PN∥DC,
∴AM=BP=EN,
又∵∠MAO=∠NOE=60°,OA=OE,
在△ONE和△OMA中,
 ,
,
∴△OMA≌△ONE(SAS),
∴OM=ON.
(3)如图3,连接OE,
由(2)得,△OMA≌△ONE,
∴∠MOA=∠EON,
∵EF∥AO,AF∥OE,
∴四边形AOEF是平行四边形,
∴∠AFE=∠AOE=120°,
∴∠MON=120°,
∴∠GON=60°,
∵∠GON=60°-∠EON,∠DON=60°-∠EON,
∴∠GOE=∠DON,
∵OD=OE,∠ODN=∠OEG,
在△GOE和∠DON中,
 ,
,
∴△GOE≌△NOD(ASA),
∴ON=OG,
又∵∠GON=60°,
∴△ONG是等边三角形,
∴ON=NG,
又∵OM=ON,∠MOG=60°,
∴△MOG是等边三角形,
∴MG=GO=MO,
∴MO=ON=NG=MG,
∴四边形MONG是菱形.
考点:四边形综合题.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案