题目内容
8.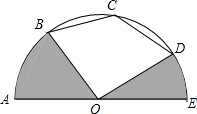 如图,半圆O的直径AE=4,点B、C、D均在半圆上,若AB=BC,CD=DE,连接OB、OD,
如图,半圆O的直径AE=4,点B、C、D均在半圆上,若AB=BC,CD=DE,连接OB、OD,(1)求证:$\widehat{AB}$+$\widehat{DE}$=$\widehat{BC}$+$\widehat{CD}$;
(2)求∠BOD度数;
(3)求图中阴影部分面积.
分析 (1)根据AB=BC,CD=DE,得到$\widehat{AB}=\widehat{BC}$,$\widehat{CD}=\widehat{DE}$,即可得到结论;
(2)根据$\widehat{AB}$+$\widehat{DE}$=$\widehat{BC}$+$\widehat{CD}$;即可得到∠BOD=$\frac{1}{2}×180°=90°$;
(3)根据扇形的面积公式即可得到结论.
解答 (1)证明:∵AB=BC,CD=DE,
∴$\widehat{AB}=\widehat{BC}$,$\widehat{CD}=\widehat{DE}$,
∴$\widehat{AB}$+$\widehat{DE}$=$\widehat{BC}$+$\widehat{CD}$;
(2)解:∵$\widehat{AB}$+$\widehat{DE}$=$\widehat{BC}$+$\widehat{CD}$;
∴∠BOD=$\frac{1}{2}×180°=90°$;
(3)由(2)得:
S阴影=S扇形OBD=$\frac{90π×(4÷2)^{2}}{360}$=π.
∴阴影部分面积为π.
点评 本题考查了扇形的面积计算及圆心角、弧之间的关系.解答本题的关键是得出阴影部分的面积等于扇形BOD的面积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.下列汽车标志的图形是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |