Question

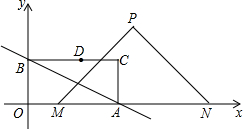
如图，抛物线y=a（x-h）²+k经过点A（0，1），且顶点坐标为B（1，2），它的对称轴与x轴交于点C．
（1）求此抛物线的解析式．
（2）在第一象限内的抛物线上求点P，使得△ACP是以AC为底的等腰三角形，请求出此时点P的坐标．

Answer 1

考点：二次函数综合题

专题：

分析：（1）由抛物线y=a（x-h）²+k的顶点坐标是B（1，2）知：h=1，k=2，则y=a（x-1）²+2，再把A点坐标代入此解析式即可；
（2）易知△OAC是等腰直角三角形，可得AC的垂直平分线是直线y=x，根据“线段垂直平分线上的点到线段两个端点的距离相等”知直线y=x与抛物线的交点即为点P，解方程组即可求出P点坐标．

解答：解：（1）∵抛物线y=a（x-h）²+k顶点坐标为B（1，2），
∴y=a（x-1）²+2，
∵抛物线经过点A（0，1），
∴a（0-1）²+2=1，
∴a=-1，
∴此抛物线的解析式为y=-（x-1）²+2或y=-x²+2x+1；

（2）∵A（0，1），C（1，0），
∴OA=OC，
∴△OAC是等腰直角三角形．
过点O作AC的垂线l，根据等腰三角形的“三线合一”的性质知：l是AC的中垂线，
∴l与抛物线的交点即为点P．
如图，直线l的解析式为y=x，
解方程组

y=x y=-x2+2x+1

，
得

x= 1+ 5 2 y= 1+ 5 2

或

x= 1- 5 2 y= 1- 5 2

，不合题意舍去），
∴点P的坐标为（

1+ 5

2

，

1+ 5

2

）．

点评：本题是二次函数的综合题型，其中涉及到的知识点有运用待定系数法求直线、抛物线的解析式，等腰直角三角形的判定与性质，两函数图象交点坐标的求法，二次函数与一元二次方程的关系，综合性较强，难度适中．