��Ŀ����
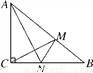
��ͼ����Rt��ABC�У���ACB��90�㣬AC��6cm��BC��8cm.����M�ӵ�B��������BA������ÿ��3cm���ٶ���A�˶���ͬʱ����N�ӵ�C��������CB������ÿ��2cm���ٶ����B�˶����˶�ʱ��Ϊt�� ������MN.
������MN.
(1)����BMN���ABC���ƣ���t��ֵ��
(2)����AN��CM����AN��CM����t��ֵ��
��ϰ��ϵ�д�
�����Ŀ


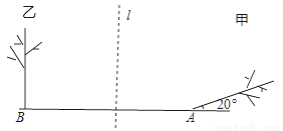
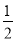 D. ��
D. ��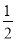

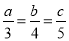 ����
����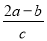 ��__________.
��__________.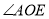 ��ƽ�ǣ�
��ƽ�ǣ� 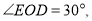
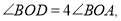 ��OCƽ��
��OCƽ��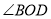 ����
����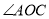 �Ķ�����
�Ķ�����